Ледяной покров состоит из льдин различных размеров и находится под совокупным воздействием термических и динамических факторов. Главной причиной неравномерности дрейфа льда за небольшие промежутки времени является большая изменчивость ветра. При увеличении временных интервалов основное влияние оказывает завихренность течений. Таким образом, скорость дрейфа льда определяется совокупностью сил, тангенциальных напряжений воды и воздуха, силы Кориолиса, течений и приливных явлений, связанных с наклоном уровня, а также сил взаимодействия льдин друг с другом и с берегом.
Тип модели для описания напряженно-деформированного состояния ледяного покрова определяется не только его свойствами как физико-географической среды, но и зависит от временной и пространственной детализации задачи [1]. Сочетание уравнений движения ледяного покрова:
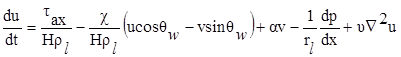 (1)
(1)
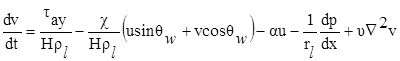 (2)
(2)
и условия несжимаемости
![]() (3)
(3)
позволяет получить для давления льдов уравнение типа Пуассона
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
где u, v - составляющие скорости дрейфа льда по осям координат;
tax, tay - составляющие касательного напряжения, действующего со стороны воздуха (ta); tw- касательное напряжение, действующее на лед со стороны воды;
Ca - коэффициент пропорциональности (0,00137) [5]; Cw - коэффициент пропорциональности (5,5) [5];
qa, qw- углы отклонения касательного напряжения от изобары (25°)[ ];
Gx, Gy, ½G½ - составляющие и модуль скорости геострофического ветра;
H, rl- толщина и плотность льда; a- параметр Кориолиса;
c=CwW, W - модуль скорости дрейфа; р - давление ледяных полей;
n- коэффициент бокового обмена импульсом.
В этом случае ледяному покрову приписываются свойства, сходные со свойствами вязкой несжимаемой пленки [11]. Будучи относительно простой, эта модель дает возможность получить поле скоростей дрейфа льда и распределение давления ледяных полей. Ранее данная модель, описанная стационарными уравнениями движения применялась для расчета ледовых сжатий [11,12].
В.И. Пономарев предложил гидродинамическую модель дрейфа льда [14]. Модель основана на классической нелинейной теории дрейфа льда, где использованы стационарные уравнения движения льда, в которых учитываются касательные силы трения на верхней и нижней границах льда, сила Кориолиса и сила горизонтального обмена импульсом.
Модель дрейфа льда представляет собой нелинейную систему алгебраических уравнений относительно составляющих скорости дрейфа u, v и напряжений трения txi, tyi на нижней и верхней границах льда:
![]() (7)
(7)
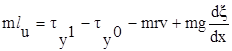 (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
где a - параметр Кориолиса; m=rlhl - масса единичного столба льда; hl - толщина льда; rl - плотность льда; величины с индексом i=1 относятся к атмосферному ППС (планетарный пограничный слой), а i=0 - к океаническому ППС; U1=u; V1=v1-v; U0=u-uh; V0=v-vh; Gi=½Ui½; u1; v1, uh, vh - соответственно составляющие скорости геострофического ветра на верхней границе атмосферного ППС и градиентного течения на нижней границе океанического ППС.
Причем Uh=gdx/dy+dur; Vh=-gdx/dx+dvr, где dx/dx, dx/dy - наклоны уровенной поверхности океана; dur, dvr - обусловленный бароклинностью сдвигающих составляющих скорости градиентного течения в пределах пограничного слоя океана при условии отсутствии льда и ветра.
Величины dx/dx, dx/dy, dur, dvr определяются с помощью диагностической модели океанической циркуляции [15], ci, ai - с помощью метода параметризации ППС [16] по заданному числу Россби и параметру стратификации mi.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.