Проблемы гидродинамики, гидрофизики и экологии крупных водоемов Сибири (Отчет по междисциплинарному интеграционному проекту фундаментальных исследований), страница 26

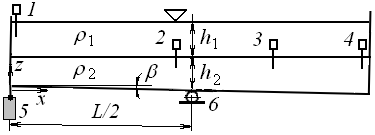
Рис. 5.4. Схема экспериментальной установки:

1-4 – волномеры, 5 - поворачивающее устройство, 6 – опора.

С помощью волномеров 1-4 (рис. 5.4) измерялись отклонения уровня свободной поверхности и границы раздела между слоями от положения равновесия (i = 1, 2, 3, 4). Принцип работы волномеров основан на различии электропроводностей жидкостей в верхнем и нижнем слое. Раствор глицерина имеет почти такую же электропроводность, как чистая вода. Для увеличения электропроводности раствора в нем растворялась соль NaCl в количестве 0.5 – 0.7 г/л. Поскольку малые вариации количества этой соли существенно влияли на калибровочные характеристики волномеров, их калибровка осуществлялась непосредственно на экспериментальной установке перед началом и в конце каждого опыта. Волномеры регистрировали суммарные колебания, обусловленные различными собственными модами.

Чтобы выделить частоты отдельных мод, выполнялся спектральный анализ функций  с использованием алгоритма быстрого преобразования Фурье. Соответствующий анализ выполнялся с помощью программного обеспечения Origin.

Выполнены две серии опытов: с переводом бассейна из горизонтального положения в наклонное и из наклонного положения в горизонтальное. В первом случае параметры сейшевых колебаний можно определить только численными расчетами, например, на основе изложенного выше метода. В случае прямоугольного бассейна с горизонтальным дном имеются явные формулы для частот сейшевых колебаний. Безразмерные модули спектров, соответствующие функциям , приведены на рис. 5.5. В спектрах четко выделяется ряд максимумов. Соответствующие им частоты для поверхностной и  для внутренней сейш (j = 1, 2, 3, . . . ) сопоставляются далее с теоретическими частотами  и  различных мод сейшевых колебаний. Значение первого максимума (на частоте) в спектре функции  использовано в качестве масштаба для всех трех спектров колебаний границы раздела. Спектр колебаний свободной поверхности нормирован на величину первого максимума в этом спектре.

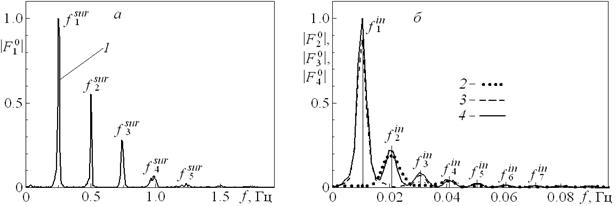
Рис. 5.5. Модули спектров функций ,, , .

Результаты сравнения эксперимента и теории по частотам колебаний показаны на рис. 5.6,

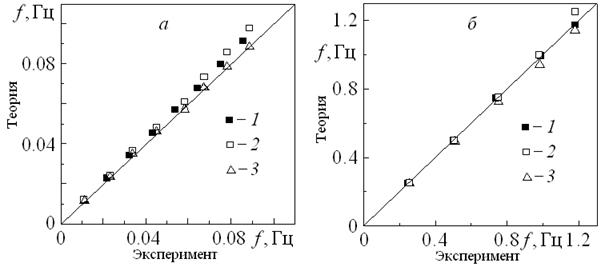
Рис. 5.6. Корреляция экспериментальных и расчетных частот сейшевых колебаний для внутренней сейши (а) и для поверхностной сейши (б): 1 - наклонное дно, 2 – горизонтальное дно (расчет на основе длинноволнового приближения), 3 – горизонтальное дно (расчет на основе строгого дисперсионного соотношения).

Дискретные точки удовлетворяют условию n = j. Приведены три группы дискретных точек. Точки 1 относятся к случаю наклонного дна при. Точки 2 и 3 относятся к случаю горизонтального дна. Прямая линия на рис. 5.6 - биссектриса координатного угла. Абсциссы дискретных точек на рис. 5.6 соответствуют экспериментальным частотам, полученным описанным выше способом. Ординаты точек, обозначенных цифрой 1, получены расчетом в длинноволновом приближении по приведенной выше теории. Ординаты точек 2 и 3 получены расчетным путем. При этом в расчетах ординат точек 2 использовалось длинноволновое приближение, а точек 3 - строгое дисперсионное соотношение линейной теории для двухслойной жидкости со свободной поверхностью.

При идеальной корреляции экспериментальных и теоретических данных дискретные точки ложатся на биссектрису координатного угла. В случае внутренней сейши (рис. 5.6, а) почти идеальная корреляция получена только для горизонтального бассейна и при использовании в расчетах строгого дисперсионного соотношения. Это свидетельствует, в частности, о надежности экспериментальных данных. Дискретные точки на рис. 5.6, а, абсциссы которых получены на основе длинноволнового приближения, систематически отклоняются вверх от биссектрисы. Для шести первых мод расчетные частоты превышают экспериментальные на 6 – 7%.