Проблемы гидродинамики, гидрофизики и экологии крупных водоемов Сибири (Отчет по междисциплинарному интеграционному проекту фундаментальных исследований), страница 23

В настоящее время существует обширная литература по наблюдениям внутренних сейш в реальных водоемах и предложены различные методы расчетов их периодов и внутренней структуры. Достаточно подробно исследованы многие зарубежные водоемы, однако озера России, особенно в восточной ее части, еще мало изучены. В данной работе представлено сравнение различных моделей, используемых для расчета внутренних сейш, на примере одного из поперечных сечений Телецкого озера. Результаты для непрерывной стратификации в реальном бассейне сопоставлены с результатами для бассейна постоянной глубины, а также моделями двухслойной и трехслойной жидкости.

Рассматривается плоская задача о свободных колебаниях устойчиво стратифицированной жидкости в бассейне переменной глубины. В вертикальной плоскости Oxz бассейн занимает область 0 ≤ x ≤ L, −H(x) ≤ z ≤ 0, где x - горизонтальная, а z – вертикальная координата, отсчитываемая вверх от невозмущенного положения верхней границы жидкости z = 0; H(x) > 0 - глубина бассейна в невозмущенном состоянии.

Линеаризованная система уравнений Эйлера для несжимаемой жидкости без учета эффектов вращения Земли имеет вид

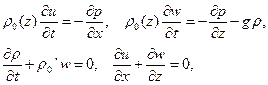                                                               (5.1)

где u(x, z, t) и w(x, z, t) - горизонтальная и вертикальная компоненты скорости;  - плотность жидкости в невозмущенном состоянии; p(x, z, t) и(x, z, t) - возмущения давления и плотности (от стационарного гидростатического состояния); g - ускорение силы тяжести; штрих означает дифференцирование по z; t - время.

Для исследования внутренних сейш верхняя граница жидкости обычно считается твердой крышкой, так как вертикальные смещения свободной поверхности во внутренних волнах малы. Это предположение приводит к следующему граничному условию:

w = 0 (z = 0).

Введение этого условия позволяет отфильтровать поверхностные сейши без существенного искажения внутренних сейш.

На дне ставится условие непротекания жидкости

Введем гармоническую зависимость по времени

где - подлежащая определению частота свободных колебаний жидкости в бассейне (частота сейши).

Используя функцию тока  , определяемую выражениями

систему уравнений (5.1) можно свести к одному уравнению

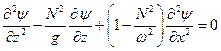                                                  (5.2)

с граничными условиями

                                                               (5.3)

Здесь - частота плавучести.

Используя приближения Буссинеска и модель длинных волн, уравнение (5..2) сведем к виду

                                                                        (5.4)

с граничными условиями (5.3).

Численные расчеты были выполнены для одного из поперечных сечений Телецкого озера. Выбранное сечение расположено в районе пос. Яйлю на расстоянии 26.2 км от с. Артыбаш и представляет собой типичный разрез в глубоководной части озера, которая занимает около половины площади озера. Измерения температуры по глубине произведены в августе 2011 года. Распределение глубины в данном сечении и температурный профиль показаны на рис. 5.1. Ширина сечения составляет L = 3.897 км, его площадь - S = 0.6868, средняя глубина - = S/L = 176.2 м, максимальная глубина - Hmax = 250 м. Существенное изменение температуры по глубине происходит только в верхнем слое жидкости (толщиной примерно 60 м). Распределение температуры в верхнем слое жидкости представлено на рис.5.2, а. Были введены различные приближения исходного распределения температуры.

Рис. 5.1. Распределение глубины (а) и температуры (б) в бассейне.

1) Детальная аппроксимация реального распределения температуры ломаной линией, что приводит к кусочно-постоянному изменению квадрата частоты плавучести по глубине. На рис. 2, б представлено изменение по глубине отношения  к максимальному значению =6.3611*10−4, т.е. При z < −70 м полагается N(z) = 0.