Проблемы гидродинамики, гидрофизики и экологии крупных водоемов Сибири (Отчет по междисциплинарному интеграционному проекту фундаментальных исследований), страница 24

2) Двухслойная жидкость с глубиной верхнего слоя 27.2 м и температурами в верхнем и нижнем слоях соответственно  и .

3) Трехслойная жидкость с глубинами верхнего и среднего слоев соответственно 20 м и 37 м и температурами в слоях , ,.

Профили температуры для двухслойной и трехслойной стратификации показаны на рис. 2,а.

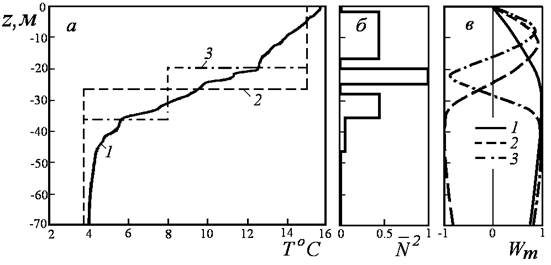
Рис. 5.2.

(а) - Распределение температуры в верхнем слое жидкости : 1 - исходный профиль, 2 - модель двухслойной жидкости, 3 - модель трехслойной жидкости;

(б)-  изменение по глубине;

(в) - собственные функции  (m = 1, 2, 3) для прямоугольной области.

Во всех трех рассмотренных случаях периоды внутренних сейш были сопоставлены с их значениями, полученными для прямоугольного бассейна, глубина которого соответствовала средней глубине данного сечения .

В случае непрерывной стратификации для численного решения уравнения (5.4) с граничными условиями (5.3) использовался метод конечных разностей. Ориентиром для поиска собственных частот основных мод сейшевых колебаний может служить решение для прямоугольного бассейна, глубина которого равна, а распределение частоты плавучести  соответствует исходному в пределах этой глубины. Вид первых трех собственных функций (m = 1, 2, 3) представлен на рис. 5.2, в. Собственные функции нормированы таким образом, что максимальное по абсолютной величине значение равно 1. В отличие от поверхностных сейш, которые характеризуются только значением n, соответствующим числу узлов по горизонтали в вертикальных смещениях свободной поверхности, тип внутренней сейши определяется двумя параметрами, для которых обычно используется обозначение VmHn.

Периоды внутренних сейш  (час) показаны в таблице 5.1, где столбцы I и II соответствуют непрерывно стратифицированной жидкости, столбцы III и IV - двухслойной жидкости, а столбцы V и VI - трехслойной жидкости. В нечетных номерах столбцов приведены результаты для реального бассейна, а в четных - для эквивалентной прямоугольной области. Видно, что в каждом из трех рассмотренных случаев стратификации жидкости периоды внутренних сейш для реального бассейна и эквивалентной ему прямоугольной области достаточно близки. В двухслойной жидкости существуют только внутренние сейши типа V1Hn (n=1,2,…). Модель трехслойной жидкости является более общей и дает возможность также оценить поведение колебаний типа  V2Hn (n=1,2,…). Как и следовало ожидать, приближение трехслойной жидкости дает более точные результаты, чем двухслойное приближение.

Таблица.5.1

Изолинии функции тока в реальном бассейне при непрерывной стратификации показаны на рис. 5.3, а-г для внутренних сейш типов V1H1, V1H2, V2H1, V2H2 соответственно. Линии тока на фиг. 5.3, б-г приведены с шагом 0.2. Функция тока в каждом из рассмотренных случаев нормирована так, что максимальное значение равно 1. Крестиками на фиг. 5.3, а-г отмечены положения этих точек. В точках, соответствующих локальным экстремумам функции тока, жидкость покоится. Положение экстремальных точек по глубине бассейна согласуется с локальными экстремумами собственных функций, представленных на фиг. 5.2, в.

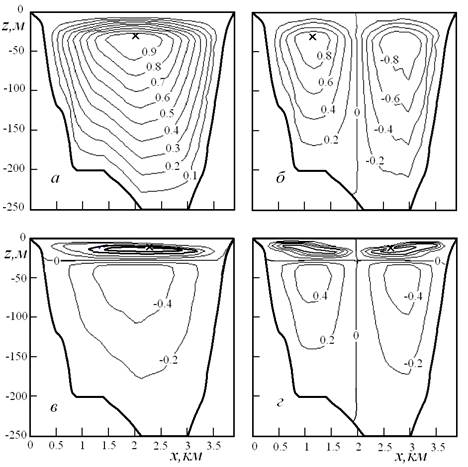
Рис. 5.3. Изолинии функции тока  для низших мод внутренних сейш:

а - V1H1, б –V1H2, в –V2H1, г - V2H2.