Проблемы гидродинамики, гидрофизики и экологии крупных водоемов Сибири (Отчет по междисциплинарному интеграционному проекту фундаментальных исследований), страница 25

Поведение изолиний функции тока наглядно демонстрирует циркуляцию жидкости внутри замкнутого бассейна, что обеспечивает водообмен между поверхностными и глубинными слоями жидкости.

В отличие от поверхностных сейш внутренние сейши носят сезонный характер и существенным образом зависят от распределения температуры в верхнем слое жидкости. К сожалению, в настоящее время практически отсутствуют натурные измерения внутренних сейш в Телецком озере. Проведенные исследования будут полезны при выполнении таких измерений в будущем.

5.2. Сейшевые колебания в бассейне, заполненном двухслойной жидкостью

Теоретически и экспериментально исследованы поверхностные и внутренние сейши в прямоугольном наклонным бассейне, заполненном двухслойной жидкостью. При теоретическом анализе использовалась линейная теория длинных волн. Жидкость предполагалась невязкой и несжимаемой.

Наиболее простой моделью плотностной стратификации является двухслойная жидкость, в которой верхний слой жидкости имеет плотность , а нижний слой – плотность . В случае длинного и узкого водоема можно использовать одномерную модель в следующем виде

                          (5.5)

                                                               (5.6)

Здесь за ось x с началом на одном из концов водоема принимается его средняя линия; (j = 1, 2) - осредненные по глубине каждого слоя горизонтальные скорости течения в верхнем (j = 1) и нижнем (j = 2) слоях; (x, t), (x, t) - смещения свободной поверхности жидкости и границы раздела слоев от горизонтальных положений соответственно;   и - безразмерные параметры, характеризующие плотностную стратификацию жидкости; - площади поперечного сечения водоема, перпендикулярного к его средней линии, в каждом из слоев; и  - ширины поперечного сечения на уровне свободной поверхности и границы раздела, соответственно; t - время.

На границах бассейна x = 0, L (L - длина средней линии) задаются условия непротекания жидкости

В результате интегрирования уравнений (5.5), (5.6) и введения новых переменных  система уравнений (5.5), (5.6) принимает вид

                                                                (5.7)

                                          (5.8)

Рассмотрим гармонические по времени колебания двухслойной жидкости в виде

                                               (5.9)

где  - подлежащая определению частота свободных колебаний жидкости в бассейне.

Подстановка (5.9) в систему уравнений (5.7), (5.8) приводит к одномерной краевой задаче для обыкновенных дифференциальных уравнений

                                                               (5.10)

                                         (5.11)

                                                                    (5.12)

Решение этой задачи получено численно конечно-разностным методом. В случае, когда значения  постоянны вдоль средней линии бассейна, решение задачи (5.10), (5.11) удается найти аналитически. Существуют две бесконечные последовательности частот собственных колебаний жидкости  и  соответственно для поверхностных и для внутренних сейш:

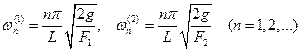, где

.

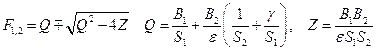Частоты , соответствующие поверхностным сейшам, слабо зависят отплотностной стратификации, тогда как частоты внутренних сейш существенно зависят от относительного перепада плотности между слоями.

Было проведено сопоставление этих теоретических результатов с полученными в процессе выполнения проекта экспериментальными данными. Схема экспериментальной установки приведена на рис. 1. Прямоугольный бассейн из оргстекла длиной L = 1.98 м и шириной B = 0.06 м мог поворачиваться в вертикальной плоскости относительно опоры 6. Поворот осуществлялся с помощью устройства 5. Далее используется неподвижная прямоугольная система координат (x, z), показанная на рис. 5.4. Заполнение бассейна осуществлялось при горизонтальном положении его дна. Сначала создавался слой водопроводной воды с плотностью  толщиной . Затем на дно бассейна медленно выпускался раствор глицерина в воде с плотностью, и создавался более тяжелый слой толщиной . Вязкость использовавшихся слабых растворов глицерина отличалась от вязкости чистой воды не более, чем на 2%.