Проблемы гидродинамики, гидрофизики и экологии крупных водоемов Сибири (Отчет по междисциплинарному интеграционному проекту фундаментальных исследований), страница 2

Если же стратификация водоема обусловлена только градиентом солёности, то уравнение для  не учитывается, а для корреляционного момента  используется известное алгебраическое соотношение [1] - модель 2.

С применением построенных численных моделей выполнены расчеты течения в канале глубиной , обусловленного действием постоянного касательного напряжения на поверхности жидкости, в соответствии с данными лабораторного эксперимента [2].

Для вертикального распределения плотности и значения касательного напряжения на свободной поверхности рассмотрены два варианта начальных условий:

(I): , ;

(II): , .

Проанализированы два вида краевого условия для энергии турбулентности на свободной поверхности. Первый вариант связывает градиент энергии турбулентности с касательным напряжением на поверхности жидкости, а второй задает её нулевой градиент. Выполнены численные эксперименты в условиях устойчивой стратификации, обусловленной градиентом солёности при однородном распределении температуры. Установлено, что изменение условия влияет только на приповерхностные значения энергии турбулентности и скорости её диссипации, а на поведение коэффициента турбулентного обмена практически не влияют.

Численные эксперименты с моделью, учитывающей двойную стратификацию, выполнены с использованием второго краевого условия. Результаты сравнивались с расчётами, полученными по разработанной усовершенствованной модели [1]. Сопоставляя результаты расчётов по двум моделям в условиях однородного распределения температуры, можно отметить, что основные характеристики модели (энергия турбулентности, скорость её диссипации и коэффициент турбулентного обмена) достаточно близки (рис. 1.3 и 1.4).

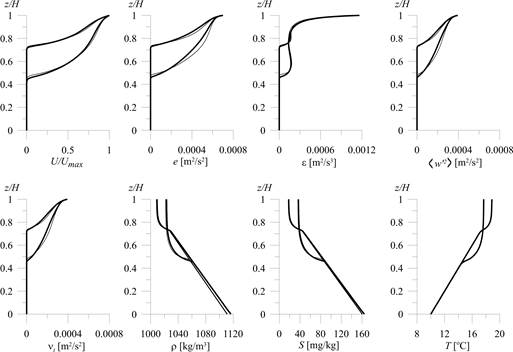
Рис.1.3. Вертикальные распределения основных параметров, полученные по модели 1 (полужирная линия) и по усовершенствованной модели [1] на моменты времени 60 с и 240 с

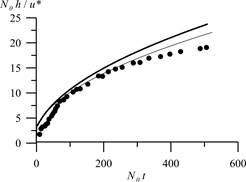
Рис. 1.4. Динамика заглубления перемешанного слоя, полученная по модели с двойной стратификацией (полужирная линия) и по "усовершенствованной модели"

В работе Вайнстока [3] предложено в случае устойчивой стратификации заменить одну из эмпирических констант , входящую в формулу корреляции "давление – градиент скаляра", функцией 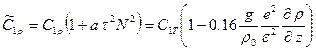 , где  – частота Вяйсяля – Брента. Численные эксперименты показали, что при использовании модели 2 с константой  и функцией  (рис. 1.5.) вертикальные распределения основных параметров несколько различаются. При этом скорость заглубления перемешанного слоя, полученная в двух расчетах, практически одинакова. Можно видеть, что диффузионные процессы менее выражены при использовании(этот вопрос требует более детального исследования).

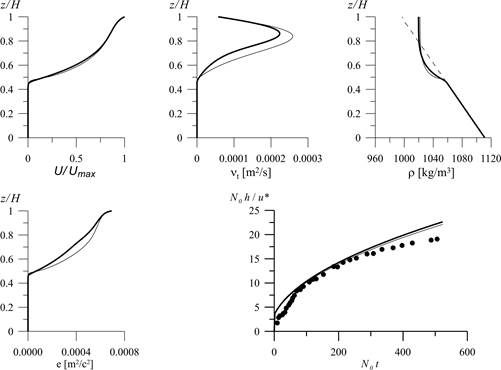
Рис. 1.5. Вертикальные распределения основных параметров на момент времени 240 с и динамика заглубления перемешанного слоя, рассчитанные по "усовершенствованной модели" с константой  (тонкая линия) и с переменной  (полужирная линия).

Использованная литература

1.  О.Ф. , Т.Э. Овчинникова, Г.Г. Черных. О численном моделировании заглубления турбулентного слоя в устойчиво стратифицированной жидкости.//Теплофизика и аэромеханика, 2013, т. 20, № 2. С. 141-152

2.  Kato H., Phillips O.M. On the penetration of a turbulent layer into stratified fluid // J. Fluid Mech. 1969. Vol. 37, part 4. P. 643-655.

3.  Weinstock J. A theory of turbulence transport. J. Fluid Mechanics, 1989, 202. P. 319–338.

Блок 2. Исследование процессов тепло - массопереноса на границах раздела вода – лед и вода – атмосфера в природных условиях и с использованием физических и математических моделей (ЛИН, ИТ, ИВЭП).

Подледный период представляют значительный интерес для динамики жидкости вследствие наличия ламинарного и переходного (ламинарно-турбулентного) режима вертикального обмена в подледном слое воды. Это дает возможность использовать покрытые льдом водоемы как «природную лабораторию» для исследований пограничного слоя. Интенсивность вертикального теплообмена в подледной воде и на границе вода-лед играет существенную роль в формировании ледового покрова, определяя темпы его нарастания и деградации.