Проблемы гидродинамики, гидрофизики и экологии крупных водоемов Сибири (Отчет по междисциплинарному интеграционному проекту фундаментальных исследований), страница 22

В ИГиЛ СО РАН в рамках первого приближения пространственно - одномерной теории мелкой воды решена задача о течениях, возникающих при разрушении плотины на скачке площади сечения прямоугольного канала (рис. 4.6), ширина которого  в верхнем бьефе () больше, чем его ширина  в нижнем бьефе ().

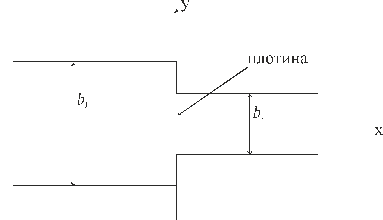
Рис. 4.6. Вид канала сверху.

Основная проблема, возникающая при решении этой задачи, заключается в том, что уравнения для полного импульса не является точным законом сохранения в случае  непризматического русла, в силу чего в рамках формальной теории мелкой воды соответствующее ему условие сопряжения на прерывной волне нельзя использовать для получения соотношения на гидродинамическом разрыве, возникающем на скачке площади сечения. Отсюда следует, что если с такого разрыва уходят две характеристик, то для замыкания соотношений на нем необходимо введение дополнительного условия. В качестве такого дополнительного соотношения используется условие, получаемое из закона сохранения локального импульса с учетом эвристического параметра, учитывающего энергетические потери на скачке площади сечения. Для определения этого эвристического параметра проведено сравнение одномерных решений с результатами численного моделирования данной задачи на основе пространственно двумерных (плановых) уравнений теории мелкой воды.

На рис. 4.7 приведены профили двух качественно различных автомодельных решений, получаемых при решении данной задачи. Пунктирными линиями показаны решения, построенные без учета потерь энергии на скачке площади сечения, а сплошными линиями – с учетом таких потерь. Буквой S на рисунках отмечены стационарные прерывные волны, распространяющиеся с постоянной скоростью по невозмущенному фону глубины , буквами  и  – центрированные волны понижения и буквой  – неподвижные гидродинамические прыжки, формирующиеся на скачке площади сечения канала. Решение, приведенное на рис. 4.6а, соответствует докритическому потоку в области постоянного течения за фронтом прерывной волны, а решение, приведенное на рис. 4.6б, – сверхкритическому потоку в этой области.

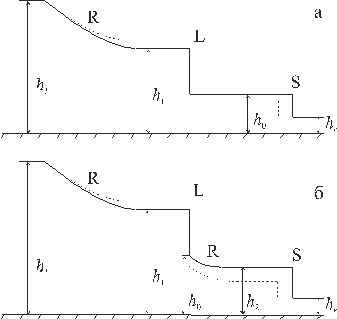
Рис. 4.7. Профили течения, возникающего при решении задачи о распаде разрыва на скачке площади сечения канала:

а) докритический поток за фронтом прерывной волны,

     б) сверхкритический поток за фронтом прерывной волны.

На рис 4.8 для случая, когда  приведено сравнение точных автомодельных решений с результатами численного моделирования этой задачи на основе пространственно - двумерных (плановых) уравнений теории мелкой воды.

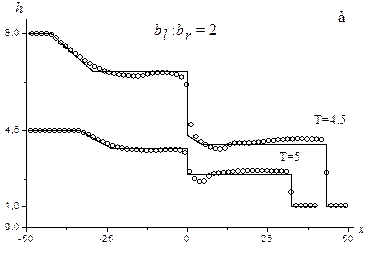
Рис. 4.8. Сопоставление решений

Сплошными линиями показаны точные решения, кружками – результаты численных расчетов. Нижний график соответствует решению с докритическим потоком в области постоянного течения за фронтом прерывной волны, а верхний – сверхкритическому потоку в этой области. Результаты опубликованы в Изв. РАН. МЖГ. 2013. № 3. С. 12-23.

Проведено сравнение построенных точных автомодельных решений с результатами моделирования этой задачи в лабораторном лотке. Это сравнение показало достаточно хорошее согласование теории с результатами лабораторных экспериментов по возможным типам волн, скорости их распространения и асимптотическим глубинам за их фронтами.

Блок 5. Сейши на озерах и водохранилищах Сибири (ИГиЛ).

5.1. Внутренние сейши в водоеме, заполненном непрерывно стратифицированной жидкостью

Внутренние сейши представляют собой свободные стоячие волны, которые возникают в замкнутых или полузамкнутых бассейнах, заполненных стратифицированной жидкостью. В природных водоемах (например, озерах) стратификация вызвана, как правило, сезонным нагревом верхнего слоя воды. Различные возмущения, действующие на водную массу, такие как ветер, сильный дождь, резкое изменение атмосферного давления, сейсмические воздействия, выводят из равновесия разноплотностные слои воды. После прекращения действия возмущения возникают внутренние сейши, в которых слои колеблются около своего положения равновесия. Большое значение внутренние сейши имеют для экологии озер, так как они приводят к перемешиванию водных масс и перераспределению кислорода и питательных веществ в водной среде.