Экономика и менеджмент \ Финансы, деньги и кредит

Гроші та кредит: Методичні вказівки до виконання практичних завдань, страница 8

Для врахування інфляції використовують наступні показники:

  рівень інфляції;

  індекс інфляції.

Рівень інфляції показує на скільки процентів виросли ціни за період часу, що розглядається:

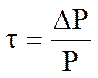                                                                ,                                            (16)

де  - рівень інфляції за певний період часу;

    P - сума грошей до інфляції (тобто первісна сума грошей);   

   DP - сума грошей, на яку треба збільшити  S,  щоб  купівельна  спроможність P+DP після інфляції дорівнювала купівельній спроможності суми грошей S до інфляції.

Тоді сума, купівельна спроможність якої з врахуванням інфляції відповідає купівельній спроможності суми S, визначається таким чином:

                                                                   (17)

Індекс інфляїціїпоказує в скільки разів збільшилися ціни за період часу, що розглядається:

                                                                                                             (18)

Якщо треба визначити рівень інфляції за деякий період часу на базі значень індексів інфляції за менші проміжки часу (за місяць), використовують таку формулу:

                                                                             (19)

  При однакових рівнях інфляції і однакових періодах ця формула здобуває такого виду:

                                                                                                         (20)

  При врахуванні інфляції в грошово – кредитних відносинах виникає проблема визначення реальної ставки проценту, що забезпечить реальну ефективність кредитної операції при рівні інфляції за строк кредиту .

Ставка проценту по кредиту, що враховує інфляцію, визначається за такими формулами:

  для простих процентів

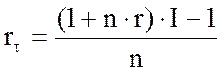                                                      ,                                    (21)

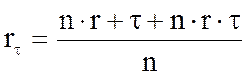або                                                ,                                 (22)

де r – потрібна реальна ефективність кредитної операції;

I, - відповідно індекс та рівень інфляції за строк кредиту;

    - ставка кредитної операції з врахуванням інфляції;

n– період кредиту в роках.

  для складних процентів

                                                      ,                                        (23)

  Значення суми вкладу, визначене з врахуванням рівня інфляції  (тобто її купівельна спроможність) за період зберігання вкладу буде визначатися за формулою:

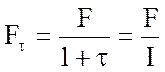                                                      ,                                            (24)

де  - сума, яку передбачається отримати по той чи іншій схемі нарахування процентів з врахуванням інфляції.

Для простих процентів накопичена сума вкладу з процентами без врахування інфляції визначаються за формулою (5): .

          З врахуванням інфляції цю формулу можна записати наступним чином:

                 (25)

Для складних процентів накопичена сума вкладу з процентами без врахування інфляції визначаються за формулою (6): .

          З врахуванням інфляції цю формулу можна записати наступним чином:

                      (26)

          Тоді для строку зберігання вкладу в 1 рік отримуємо:

                                             (27)

          Залежність, наведена формулою (27) носить назву формули Фішеру та дозволяє визначити річну ставку кредитної операції з врахуванням інфляції (ставка - брутто) при рівні інфляції за рік   та бажаній реальній доходності кредитної операції r (ставка - нетто). Значення  називають інфляційною премією.

Приклади рішення базових задач.

  Приклад 1. Маса товарів у обороті оцінюється в 58 млрд. дол.  Угоди в кредит, термін сплати за якими ще не наступив, складають 13 млрд., строкові платежі - 10,5,    платежі, що взаємопогашаються - 4,5 млрд. дол.  В обіг випущено 12 млрд. дол. у формі золотих монет.  Середнє число оборотів грошової одиниці - 6.  Скільки золота пішло в скарб?  

Рішення.  

Гоб   =   (58 -  13 + 10,5  - 4,5) : 6  = 8,5 млрд. дол.

В скарб пішло 3,5 млрд. дол. (12 – 8,5 = 3,5 млрд. дол.)

Приклад 2. Ціни зростають кожен місяць на 8 %. Визначити рівень та індекс інфляції зі рік. Що це означає?

Рішення.

1) Індекс інфляції складе:

 

2) Рівень інфляції складе:

Висновок: за рік ціни зростуть у 2,52 рази, або на 152 %.

Приклад 3.  Фірма А на депозитному рахунку в I банку зберігає 400 тис. грн. Ці гроші внесено на рахунок 1.01 під 36 % річних з нарахуванням щомісячно складних процентів. У другому банку фірмою 1.02 розміщено на депозитному рахунку 550 тис. грн. під 24 % річних з нарахуванням щомісячних складних процентів. 1.07 фірма планує придбати устаткування вартістю 1 млн. гривень. Ця ціна встановлена на 1.01. Ціна устаткування, за якою продавець згоден буде його продати повинна враховувати інфляцію за цей проміжок часу. Рівень інфляції становив за цей період (%): січень - 2,0; лютий – 2,1; березень – 2,2; квітень – 2,2; травень – 2,4; червень – 2.

Визначити достатність на депозитних вкладах грошових коштів разом з процентами для купівлі устаткування.

Якою буде купівельна спроможність вкладів з урахуванням процентів та інфляції?

Рішення.

1) Сума банківського вкладу разом з процентами в першому та другому банку відповідно становитиме:

400 ∙ (1 + 0,36/12)12∙6/12 = 477,62 тис. грн.

550 ∙ (1 + 0,24/12)12∙5/12  = 607,24 тис. грн.

å 1084,86 тис. грн.

2) Індекс інфляції за період зберігання вкладів в першому та другому банку відповідно становитиме:

І1 = 1,02∙1,021∙1,022∙1,022∙1,024∙1,021 = 1,1372.

І2 = 1,021∙1,022∙1,022∙1,024∙1,021 = 1,1149.

3) Ціна устаткування з урахуванням інфляції становитиме:

1,0∙1,1372 = 1,1372 млн. грн.

4) Купівельна спроможність вкладів на 1.07 становитиме:

Вклад у першому банку: 477,62 тис. грн.:1,1372 = 420,0 тис. грн.

Скачать файл