В современной технической литературе часто используется математическое описание различных объектов в относительных величинах. Приведем к такому виду исходные уравнения электромеханического преобразователя (3.1) – (3.5) с целью, во-первых, научиться это делать и, во-вторых, познакомиться с преимуществами и недостатками относительных величин.
Начнем с того,
что введем некоторые базовые значения переменных, обозначив их соответствующей
заглавной буквой с индексом «б»: 
. Часть базовых переменных
можно ввести независимо, а часть окажутся зависимыми через уравнения (3.1) – (3.5).
Так, введя независимо 
и 
, базовые значения напряжения
(ЭДС) и момента можно определить: 
, 
Напротив, при задании 
и 
зависимым
окажется 
и т. д.
Часто, хотя это
и необязательно, в качестве базовых величин выбирают номинальные величины
двигателя. Мы поступим так же и выберем в качестве независимых базовых величин:
. Тогда соответственно 
и 
.
Разделив все члены (3.2) на 
, получим:
,
(3.12)
где звездочками отмечены
безразмерные переменные, т.е. отнесенные к базовым, 
.
Постоянная
времени цепи возбуждения 
как и
само время, сохранила единицы «секунды». Можно и эти величины сделать
безразмерными, введя какую-либо базовую величину 
для
времени. Тогда будем иметь безразмерное время 
и
соответственно безразмерную постоянную времени 
.
Разделив обе
части (3.1) на 
, получим:
,
(3.13)
где 
, или, если зависимость 
нелинейна, то ее вид в
безразмерной форме, такой же, как на рис. 3.3,а.
Таким образом, когда ясна процедура, легко записать в безразмерных переменных и оставшиеся уравнения (3.3) – (3.5):
;
(3.14)
;
(3.15)
;
(3.16)
где:
В (3.14) можно, как и в (3.12), избавиться от размерного времени.
Посмотрим, что
мы выиграли и что проиграли в новой записи уравнений в сравнении с исходной.
Во-первых, модель стала более компактной: одинаковой для всех подобных машин
стала зависимость 
; из уравнений
исключен конструктивный коэффициент k. Во-вторых,
все переменные не имеют размерности, изменяются в небольших пределах. Особенно
это удобство заметно, если рассматривать модель при фиксированных значениях
некоторых величин, например при номинальном напряжении якорной цепи и
номинальном потоке. Тогда (3.14) – (3.16) примут вид:
;
;
.
Приняв р = 0(установившийся режим), будем иметь при этом условии очень простое выражение
для механической 
или
электромеханической 
характеристик:
.
(3.17)
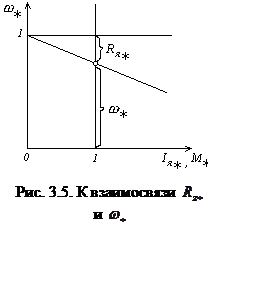Положив в
(3.17) ток якоря равным номинальному 
(вертикаль
на рис. 3.5), обнаруживаем, что сопротивление якорной цепи равно относительному
перепаду скорости:
.
(3.18)
Это простое
соотношение позволяет при известном 
очень
легко строить характеристику и, наоборот, зная желаемую характеристику,
определять соответствующее ей 
. и,
следовательно, 
. Напомним, что все
это верно при 
и 
.
К недостаткам модели в относительных величинах следует отнести ее некоторую «безликость», в ней утрачивается представление о реальных величинах: токах, моментах, скоростях и др. По-видимому, следует пользоваться и тем, и другим видом динамических моделей – в теоретических задачах удобнее «безразмерная» модель, в практических реализациях от нее следует переходить к конкретным физическим величинам.
Полученная в разделе 3.2 модель машины постоянного тока служит основой для
построения различных электроприводов, использующих этот тип электромеханического
преобразователя. Рассмотрение этих электроприводов начнем с общего случая,
когда машина имеет независимое возбуждение, т.е. цепь якоря и цепь возбуждения
раздельно подключаются к каким-либо электрическим устройствам,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.