Основные понятия и определения в электроприводе. Механическая часть силового канала электропривода. Физические процессы в электроприводе с машинами постоянного тока, страница 15

компенсационные обмотки, в связи с чем под  понимают суммарное сопротивление всех указанных элементов, т.е. .

Лучше всего иметь каталожное значение , приведенное к рабочей температуре двигателя, либо определить  непосредственным измерением, однако на практике и то, и другое не всегда возможно и приходится прибегать к косвенным оценкам. Величину  можно приближенно оценить, положив, что половина номинальных потерь  –  это потери в якорной цепи, т.е.

.                                                (3.6)

Тогда, учитывая, что , имеем:

, или

                                   .                                              (3.7)

Зная сопротивление якорной цепи () или, оценив его по (3.7), можно найти непосредственно по паспортным данным очень важную величину , входящую в уравнения (3.4) и (3.5), записанные для номинального потока. Переписав (3.3) для номинального установившегося двигательного режима (), получим:

и следовательно, по (3.4) можно определить:

.                                   (3.8)

Найденное значение  позволяет определить номинальный электромагнитный момент в соответствии с (3.5):

.                                                  (3.9)

Если  было определено по (3.7), целесообразно сравнить  с номинальным моментом на валу машины . При этом должно выполняться соотношение , так как, очевидно, что , где - момент механических потерь в двигателе.

Индуктивность якорной цепи () можно приближенно ценить по формуле:

                        (3.10)

(меньшее значение соответствует компенсированным двигателям, большее – некомпенсированным).

Для оценки параметров цепи возбуждения двигателей  и  обычно требуются сведения, не приводимые в общедоступных каталогах: соединение обмоток полюсов, номинальный поток, число витков, кривая намагничивания.

На рис. 3.3,а приведена характерная для многих двигателей постоянного тока кривая намагничивания в относительных единицах, из которой следует, что индуктивность в области малых токов отличается от индуктивности вблизи  в 5 – 7 раз. В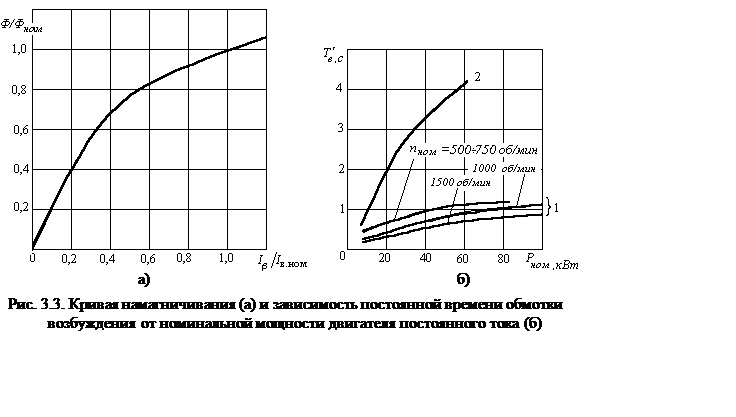
связи с этим при решении практических задач приходится учитывать конкретные пределы изменения тока возбуждения и потока.

Для грубых оценок можно воспользоваться постоянными времени цепи возбуждения , примерные значения которых для начального линейного участка кривой намагничивания приведены на рис. 3.3,б.

3.2. Варианты динамической модели

Исходные уравнения

После того, как мы познакомились с ограничениями на переменные и научились определять параметры, вернемся еще раз к исходным уравнениям машины постоянного тока (3.1) – (3.5), образующим ее динамическую модель.

В зависимости от характера задач, которые нужно решать, эти уравнения представляют в различных формах. Так, если машина войдет элементом в более сложную динамическую систему, которую предполагается анализировать с использованием структурной схемы в переменных «вход – выход», целесообразно представить уравнения (3.1) – (3.5) в виде структурной схемы машины.

В частности, если не предполагается изменять возбуждение машины, т.е.  то при входных переменных  и , и выходной М из (3.3) – (3.5) получим:

, где  – постоянная времени якорной цепи;  – оператор дифференцирования или оператор Лапласа.

Соответствующая структурная схема представлена на рис. 3.4; в ней введены следующие обозначения:   –  скорость идеального холостого хода, т.е. скорость при ;   – жесткость механической характеристики.

Структурная схема (рис. 3.4) позволяет рассматривать двигатель как объект системы автоматического управления. В теории электропривода /4, 5/ вводится понятие динамической жесткости механической характеристики, представляющей собой передаточную функцию двигателя по возмущению:

.                                (3.11)

Динамическая жесткость характеризует электромеханический преобразователь в установившемся динамическом режиме периодических колебаний скорости и момента и позволяет обоснованно судить о расхождении между статической и динамической характеристиками.

Динамическая модель