В системах электропривода основным режимом работы электрической машины является двигательный. При этом момент сопротивления имеет тормозящий характер по отношению к движению ротора и действует навстречу моменту двигателя. Поэтому положительное направление момента сопротивления принимают противоположным положительному направлению момента двигателя, в результате чего уравнение (2.8) при J = const может быть представлено в виде:
M
– Mс = J
. (2.9)
Уравнение (2.9) называют
основным уравнением движения электропривода. В уравнении (2.9) моменты являются алгебраическими, а не векторными
величинами, поскольку оба момента М и 
действуют
относительно одной и той же оси вращения.
Правую часть уравнения (2.9)
называют динамическим моментом (
), т.е.
.(2.10)
Из (2.10) следует, что направление динамического момента всегда совпадает с направлением ускорения электропривода.
В зависимости от знака динамического момента различают следующие режимы работы электропривода:
1)
> 0,
т.е. d
/dt > 0, разгон при > 0, торможение при < 0;
2)
< 0,
т.е. d/dt< 0,
торможение при > 0, разгон при < 0;
3)
= 0, т.е.
d/dt = 0, установившийся
режим, т.е. = const.
Момент, развиваемый двигателем, не является постоянной величиной, а представляет собой функцию какой-либо одной переменной, а в некоторых случаях и нескольких переменных. Эта функция задается аналитически или графически для всех возможных областей ее изменения. Момент сопротивления также может быть функцией какой-либо переменной: скорости, пути, времени. Подстановка в уравнение движения вместо М и Мс их функций приводит в общем случае к нелинейному дифференциальному уравнению.
Уравнение движения в дифференциальной форме (2.10) справедливо для постоянного радиуса инерции вращающейся массы. В некоторых случаях, например при наличии кривошипно-шатунного механизма (см. рис. 2.2, г), в кинематической цепи привода радиус инерции оказывается периодической функцией угла поворота. В этом случае можно воспользоваться интегральной формой записи уравнения движения, исходящей из баланса кинетической энергии в системе:
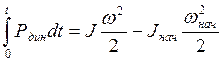, (2.11)
где 
– запас
кинетической энергии привода для рассматриваемого
момента времени; 
– начальный запас
кинетической энергии привода.
Дифференцируя уравнение (2.11)
по времени с учетом того факта, что J – функция
угла поворота 
, получаем:
. (2.12)
Так как Рдин =
, то, разделив (2.10)
на угловую скорость ω, получим уравнение
движения при J = f(φ) в следующем виде:
.
(2.13)
В ряде случаев целесообразно рассматривать движение на рабочем органе производственной машины (такие задачи часто возникают для подъемно-транспортных машин с поступательно движущимся рабочим органом). В этом случае следует использовать уравнения для поступательного движения. Уравнение движения электропривода для поступательного движения получают так же, как и для вращательного движения. Так при m = constуравнение движения принимает вид:
.
(2.14)
При m = f(l), где lвеличина пройденного рабочим органом пути, уравнение движения принимает вид:
. (2.13)
Полученные уравнения движения электропривода (2.9), (2.13), (2.14) и (2.15) позволяют решать различные динамические задачи.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.