Расчётная оценка числовых характеристик выборки. Расчётное определение параметров линейной регрессии и коэффициента корреляции

ЗАДАЧА IV. РАСЧЁТНАЯ ОЦЕНКА ЧИСЛОВЫХ ХАРАКТЕРИСТИК

Цель задачи IV. Для каждой выделенной в предварительном анализе генеральной совокупности вычислить выборочное среднее, выборочную дисперсию, выборочное среднее квадратичное отклонение, выборочные показатели асимметрии и эксцесса каждой из компонент совместного двухмерного распределения (X,Y).

Перечислим по шагам этапы решения этой задачи

Шаг 1.Вычисление начальных моментов.

Шаг 2.Вычисление центральных моментов.

Шаг3.Расчёт несмещённых оценок.

Шаг4.Числовые характеристики компоненты х и компоненты у.

«Фоновый» массив С

Для вычисления выборочного среднего , выборочного среднего квадратичного отклонения S_x, выборочных показателей асимметрии  а_х и эксцесса е_х «фонового» массива С требуется провести четыре усреднения, да ещё возвести всю выборку в степени 2, 3, 4. Для выборки приличного объёма (n=75) это большие вычисления.

В данной задаче предлагается метод с использованием «выбора ложных нулей», позволяющий резко сократить объём и время вычислений. Теоретические пояснения к задаче в прил. 2.

Шаг 1. Вычисление начальных моментов

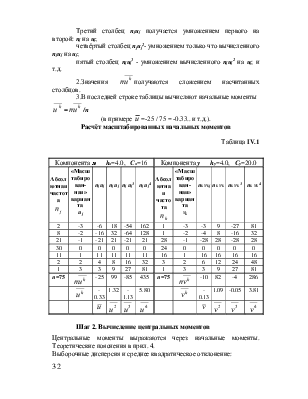
Для вычисления начальных моментов компоненты х «фонового» массива С заполним табл. IV.1.

1.В первый и второй столбцы заполняемой таблицы переносим данные (n_j, u_j) двухмерной гистограммы (табл. II.1), где u_j -  «масштабированная» варианта связанная с x_j соотношением: x=16.0+4.0u.

Третий столбец n_ju_j получается умножением первого на второй: n_j на u_j;

четвёртый столбец n_ju_j²- умножением только что вычисленного n_ju_j на u_j;

пятый столбец n_ju_j³ - умножением вычисленного n_ju_j² на u_j; и т.д.

2.Значения получаются сложением насчитанных столбцов.

3.В последней строке таблицы вычисляют начальные моменты =/n

(в примере =-25 / 75 = -0.33.. и т.д.).

Расчёт масштабированных начальных моментов

Таблица IV.1

Шаг 2. Вычисление центральных моментов

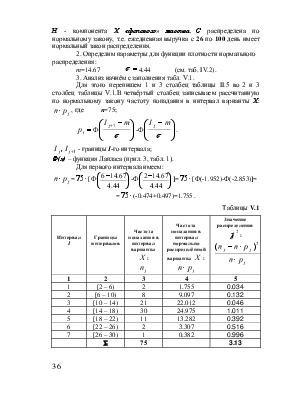
Центральные моменты выражаются через начальные моменты. Теоретические пояснения в прил. 4.

Выборочные дисперсия и среднее квадратическое отклонение:

=1.32-(0.33)²=1.21;              S_u==1.10.

Третий и четвёртый «масштабированный» центральный выборочный момент:

=-3+2³=1.13-1.32(-0.33)+2(-0.33)³=0.40;

=-4+6²-3⁴=5.80-4(-1.13)(-0.33)+1.32(-0.33)²-3(-0.33)⁴=5.14.

Шаг 3. Несмещённые оценки

Для расчёта «исправленных» центральных моментов вычислим «поправочные» коэффициенты (в «фоновом» массиве С n=75):