Расчётная оценка числовых характеристик выборки. Расчётное определение параметров линейной регрессии и коэффициента корреляции, страница 4

Шаг 2. Оценка нормального распределения компонент Х, Y по критерию А.Н. Колмогорова “аномальных” серий А и В.

«Аномальная» серия А

Компонента Х

1. Выдвинем гипотезу:

Н - компонента Х «аномальной» серии А распределена по нормальному закону, т.е. ежедневная выручка с 1 по 11 день имеет нормальный закон распределения.

2. Определим параметры для нормального распределения:

m=21.43               6.02              (см. таб. IV.2).

3. Анализ начнём с заполнения табл. V.3.

Для этого:

-  перепишем в первый столбец из таблицы А значения x_i «аномальной» серии А;

-  во втором столбце рассчитаем аргумент для функции Лапласа нормального распределения с параметрами m=21.43  и 6.02;

-  в третий столбец занесём значения функции Лапласа (прил. 3, табл.1);

-  в четвёртый столбец занесём рассчитанные значения функции распределения (см. прил. 3), при условии, что случайная величина Х распределена нормально с параметрами m=21.43  и 6.02 .

Таблица V.3

Варианты компоненты Х, xi	Аргумент ф-ции Лапласа,	Функция Лапласа,	Функция распределен, F(x)
1	2	3	4
6.29	-2.51	-0.493	0.006
16.9	-0.75	-0.258	0.242
19.1	-0.40	-0.155	0.345
20.47	-0.15	-0.059	0.441
20.79	-0.10	-0.039	0.460
23.34	0.31	0.117	0.618
24.07	0.43	0.165	0.665
24.9	0.57	0.201	0.702
26.41	0.82	0.289	0.789
26.76	0.88	0.31	0.810
26.82	0.89	0.315	0.816

4. На графике кумулятивных функций распределения вероятностей «аномальных» серий А и В компоненты х (см. рис. II.5) строим функцию нормального распределения F(x) с параметрами m=21.43  и 6.02 . График приобретает вид рис. V.1.

Кумулятивная функция распределения вероятностей «аномальной» серии Аи функция нормального распределения вероятностей F(x)

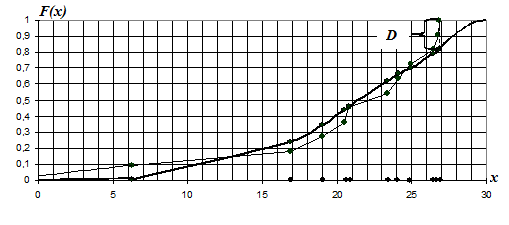
Рис.V.1

5.По графику определяем максимальную меру расхождения между кумулятивной функцией распределения вероятностей «аномальной» серии А и функцией нормального распределения F(x):

D=0.184 .

6.Расчитаем величину :              0.61 .

7.Определяем вероятность , используя табл. 2 прил. 6.

=0.86.

Вывод: эта вероятность малой не является, поэтому гипотезу Н о том, что ежедневная выручка с 1 по 11 день имеет нормальный закон распределения, можно считать правдоподобной.

Компонента Y

1. Выдвинем гипотезу:

Н - компонента Y «аномальной» серии А распределена по нормальному закону, т.е. ежедневные издержки предприятия на ед. продукции с 1 по 11 день имеют нормальный закон распределения.

2. Определим параметры для нормального распределения:

m=22.58               5.56              (см. таб. IV.2).

3. Заполним табл. V.4.

Таблица V.4

Варианты компоненты Y, yi	Аргумент ф-ции Лапласа,	Функция Лапласа,	Функция распределен, F(y)
1	2	3	4
16.75	-1.05	-0.352	0.148
18.87	-0.67	-0.250	0.250
19.33	-0.58	-0.225	0.275
19.48	-0.56	-0.208	0.291
19.5	-0.55	-0.191	0.308
20.63	-0.35	-0.136	0.363
22.22	-0.06	-0.020	0.480
23.14	0.10	0.039	0.539
23.4	0.15	0.059	0.559
28.68	1.10	0.384	0.884
36.35	2.48	0.493	0.993