4. На графике кумулятивных
функций распределения вероятностей «аномальных» серий А и В
компоненты y (см.
рис. II.5) строим функцию нормального
распределения F(y) с
параметрами m=21.58 и ![]() 5.56 . График приобретает вид рис. V.2.
5.56 . График приобретает вид рис. V.2.
Кумулятивная функция распределения вероятностей «аномальной» серии Аи функция нормального распределения вероятностей F(y)
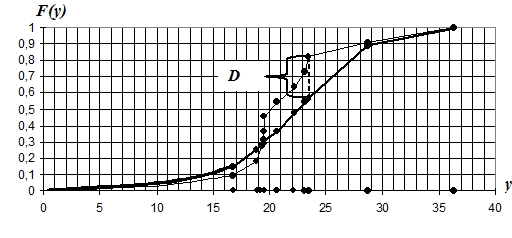
Рис.V.2
5.По графику определяем максимальную меру расхождения между кумулятивной функцией распределения вероятностей «аномальной» серии А и функцией нормального распределения F(y):
D=0.258 .
6.Расчитаем величину ![]() :
: ![]() 0.85 .
0.85 .
7.Определяем вероятность ![]() :
: ![]() =0.46.
=0.46.
Вывод: эта вероятность малой не является, поэтому гипотезу Н о том, что ежедневные издержки предприятия на ед. продукции с 1 по 11 день имеют нормальный закон распределения, можно считать правдоподобной.
Аналогично исследуется «аномальная» серия В.
Компонента Х
1. Выдвинем гипотезу:
Н - компонента Х «аномальной» серии В распределена по нормальному закону, т.е. дневная выручка с 12 по 25 день имеет нормальный закон распределения.
2. Определим параметры для нормального распределения:
m=16.67 ![]() 6.07 .
6.07 .
3.Наносим график функции распределения вероятностей F(x) нормального
закона с параметрами m=16.67
и ![]() 6.07 на рис.II.5.
6.07 на рис.II.5.
График приобретает вид рис. V.3.
Кумулятивная функция распределения вероятностей «аномальной» серии В и функция нормального распределения вероятностей F(x)

Рис.V.3
4.По графику определяем максимальную меру расхождения между кумулятивной функцией распределения вероятностей «аномальной» серии В и функцией нормального распределения F(х):
D=0.1 .
5.Расчитаем величину ![]() :
: ![]() 0.37 .
0.37 .
6.Определяем вероятность ![]() =0.999 .
=0.999 .
Вывод: эта вероятность достаточно велика, поэтому гипотезу Н о том, что дневная выручка с 12 по 25 день имеет нормальный закон распределения, можно считать правдоподобной.
Компонента Y
1. Выдвинем гипотезу:
Н - компонента Y «аномальной» серии В распределена по нормальному закону, т.е. ежедневные издержки предприятия на ед. продукции с 12 по 25 день имеют нормальный закон распределения.
2. Определим параметры для нормального распределения:
m=26.62 ![]() 6.64 .
6.64 .
3.Наносим
график функции распределения вероятностей F(x) нормального закона с параметрами m=26.62 и ![]() 6.64 на
рис.II.5.
6.64 на
рис.II.5.
График приобретает вид рис. V.4.
Кумулятивная функция распределения вероятностей «аномальной» серии В и функция нормального распределения вероятностей F(y)
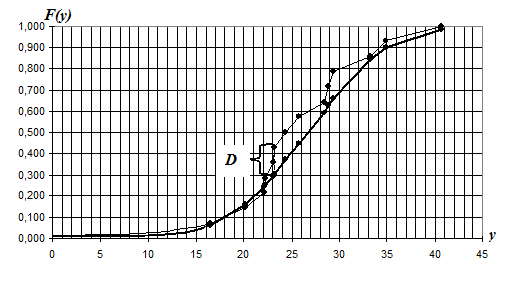
Рис.V.4
4.По графику определяем максимальную меру расхождения между кумулятивной функцией распределения вероятностей «аномальной» серии В и функцией нормального распределения F(y):
D=0.13 .
5.Расчитаем величину ![]() :
: ![]() 0.49 .
0.49 .
6.Определяем вероятность ![]() =0.96 .
=0.96 .
Вывод: эта вероятность достаточно велика, поэтому гипотезу Н о том, что ежедневные издержки предприятия на ед. продукции с 12 по 25 день имеют нормальный закон распределения, можно считать правдоподобной.
Цель задачи VI. Используя графический метод оценить зависимость между наблюдаемыми случайными величинами Х и Y.
Перечислим по шагам этапы решения этой задачи
Шаг 1.Нахождение уравнений регрессии графическим методом.
Шаг 2.Оценка ширины облака наблюдений.
Чтобы построить линии регрессии вернёмся к корреляционным полям (см. рис.II.1 и рис. II.2).
Основная цель
построения корреляционных полей («диаграмм рассеяния») – это способ «увидеть»
зависят ли ![]() и
и ![]() друг от друга. Если да, то
«облако наблюдений» тяготеет к какой-то линии (прямой или кривой). Если нет, то
«облако наблюдений» – это просто «клякса» без выраженной формы.
друг от друга. Если да, то
«облако наблюдений» тяготеет к какой-то линии (прямой или кривой). Если нет, то
«облако наблюдений» – это просто «клякса» без выраженной формы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.