Расчётная оценка числовых характеристик выборки. Расчётное определение параметров линейной регрессии и коэффициента корреляции, страница 2

=1.0135;                       =1.0413;                =1.0847;

=1,0563;    =0,0850;

затем сами «исправленные» центральные моменты

==1.0135=1.23;                            ==1.11;

==1.0413=0.42;

==5.14-0.085=5.31.

Шаг 4. Числовые характеристики выборки х

Начальные и центральные моменты х выражаются через моменты u:               ;                ,

а показатели асимметрии и эксцесса совпадают:

;                            .

Для компоненты х «фонового» массива С среднее и среднеквадратичное отклонение равны:

=16.0+4.0 (-0.33)=14.67;

S_x=h_xS_u==4.40;

==4.44.

Показатели асимметрии и эксцесса:

==;

==.

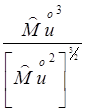Сравнивая «исправленные» значения и что было до «исправления» =1.11 и S_u=1.10;

=0.42 и =0.40;

=5.31 и =5.14

видим, что эффект «исправления» невелик и с ним можно не возиться. Однако «исправления» незначительны только для больших выборок (от n>50). На малых выборках «исправления» очень даже заметны.

Обработка у полностью аналогична.

«Аномальные» серии А и В

Обработку каждой отдельно взятой «аномальной» серии проведём аналогично обработке «фонового» массива. При расчёте асимметрии и эксцесса будем использовать несмещённые оценки.

Результаты исследования представим в виде таблицы IV.2

Таблицы IV.2

Числовые характеристики протокола наблюдений

Генеральная		Компонента х					Компонента у
	совокуность
	А		21.43	6.02	-1.73	2.29		22.58	5.56	1.77	2.06
	В		16.67	6.07	0.01	-0.43		26.62	6.44	0.69	-0.12
	С		14.67	4.44	0.31	0.51		19.48	4.17	0.35	0.40

Вывод: ежедневная средняя прибыль с 1 по 11 день составляет 21.43  тыс.руб.в среднем 6.02 тыс.руб., а ежедневные средние издержки на ед. продукции за этот период составили 22.58 руб. в среднем 5.56 руб.

Ежедневная средняя прибыль с 12 по 25 день составляет 16.67  тыс.руб.в среднем 6.07 тыс.руб., а ежедневные средние издержки на ед. продукции за этот период составили 26.62 руб. в среднем 6.44 руб.

Ежедневная средняя прибыль с 26 по 100 день составляет 14.67  тыс.руб.в среднем 4.44 тыс.руб., а ежедневные средние издержки на ед. продукции за этот период составили 19.48 руб. в среднем 4.17 руб.

ЗАДАЧА V. СРАВНЕНИЕ С НОРМАЛЬНЫМ РАСПРЕДЕЛЕНИЕМ ПО КРИТЕРИЮ ПИРСОНА И КРИТЕРИЮ КОЛМОГОРОВА

Цель задачи V. Для каждой генеральной совокупности оценить, используя критерий Пирсона или критерий А.Н.Колмогорова, соответствуют ли одномерные распределения компонент Х и Y нормальному распределению.

Перечислим по шагам этапы решения этой задачи.

Шаг 1. Оценка нормального распределения компонент Х, Y по критерию Пирсона“фонового” массива С;

Шаг 2. Оценка нормального распределения компонент Х, Y по критерию Колмогорова “аномальных” серий А и В.

Шаг 1. Оценка нормального распределения компонент Х, Y по критерию Пирсона “фонового” массива С;

Компонента Х

1. Выдвинем гипотезу:

Н - компонента Х «фонового» массива С распределена по нормальному закону, т.е. ежедневная выручка с 26 по 100 день имеет нормальный закон распределения.

2. Определим параметры для функции плотности нормального распределения:

m=14.67               4.44              (см. таб. IV.2).

3. Анализ начнём с заполнения табл. V.1.

Для этого перепишем 1 и 3 столбец таблицы II.5 во 2 и 3 столбец таблицы V.1.В четвёртый столбец записываем рассчитанную по нормальному закону частоту попадания в интервал варианты Х: , где      n=75;