Теория игр и исследование операций. Модели, алгоритмы, сложность: Конспект лекций

Ярославский государственный университет

Кафедра компьютерной безопасности
и математических методов обработки информации

ТЕОРИЯ ИГР

И

ИССЛЕДОВАНИЕ ОПЕРАЦИЙ

Модели, алгоритмы, сложность.

Конспект лекций

Ярославль, 2006

Хотели как лучше, а получилось как всегда.               

Виктор Черномырдин, премьер России в 1994-1998гг

Введение.

Термин исследование операций возник в 30-е годы ХХ века как название подразделения британских ВВС, занимавшегося планированием мероприятий противовоздушной обороны. Как самостоятельный предмет выделился в 50-х годах и включил в себя теорию принятия решений, сетевые модели, СМО и др.

Операцией называется система действий, объединенных единым планом и направленных на достижение определенной системы целей. Отличительными признаками операции являются допустимость, отражающая ограниченность ресурсов, и управляемость. Всякий допустимый выбор управляемых параметров называется решением. Цель исследования операций – предварительное количественное обоснование решений, оптимизирующих целевые функции.

ПРИМЕРЫ ЧАСТНЫХ ЗАДАЧ исследования операций:

1) Снабжение предприятий (критерий эффективности –расходы на 1 ед. сырья).

2) Постройка участка магистрали (цели - быстрее закончить, уложиться в срок).

3) Продажа сезонных товаров.                    4) Расчистка дорог от снега.

5) Медицинское обследование.                   6) Противолодочный рейд.

ОСНОВНЫЕ ЭТАПЫ ОПЕРАЦИОННОГО ИССЛЕДОВАНИЯ.

1.  Неформальная постановка задачи.

2.  Построение математической модели исследуемой системы, т.е. выбор признаков, существенных для принятия решений, и связей между ними.

3.  Выбор критериев оптимизации, т.е. выбор функций f_i(x,…).

4.  Имеет ли поставленная математическая задача приемлемые методы решения? Если нет Þ упрощаем модель или выбираем другие критерии.

5.  Находим решение в рамках модели.

6.  Проверка адекватности решения. Если решение неадекватно, то уточняем модель, вводя какие-либо дополнительные ограничения. Здесь требуется эксперт (критерий), способный оценить адекватность получаемых решений.

Даже если в результате исследования удается найти наилучшее решение, окончательный выбор должен делать человек, используя дополнительную информацию, не отраженную в модели. Сложность исследования состоит в подборе подходящей модели и четком формулировании целей операции.

КЛАССИФИКАЦИЯ ЗАДАЧ ИО по постановке и методам решения :

К случаю, когда D – плохо структурировано (например, целочисленно) относится большинство NP-полных задач. Для их решения используется точный метод ветвей и границ или работающие более быстро приближенные методы.

В многокритериальных задачах цели могут оказаться противоречивыми, поэтому внимание сосредотачивается на выборе критериев.

a)  Выбор главного критерия, т.е. f _i0 ® extrпри ограничениях  для i¹i₀.

b)  Построение свертки критериев  F(x)= · f(x), где a_i – вес i-гокритерия.

c)  Принцип Парето (отсечение вариантов, более слабым по всем показателям).

При принятии решений в условиях неопределенности функция fзависит от неизвестного y, от которого можно избавиться следующими способами:

a)  Пессимист: F(x)= f(x,y). Пример – строительство моста.

b)  Оптимист: F(x)= f(x,y). Пример - снятие вратаря в хоккее.

c)  Прагматик: F(x)= M_y f(x,y), здесь y рассматривается как случайная величина и M_y  – оператор мат.ожидания по y. Теперь x^опт=argmaxF(x) .

В играх имеется несколько активных сторон (игроков), поведение которых описывается множествами стратегий. Некоторые игроки делают выбор случайно, а остальные стремятся максимизировать свои функции полезности. Для определения наиболее разумного поведения игроков применимы принципы Парето, пессимиста (когда действия других игроков неизвестны) и Нэша (или равновесия) – когда всем игрокам невыгодно играть по-другому.

Заметим, что модель принятия решений в условиях неопределенности иногда интерпретируется как игра с природой.

Типы рекуррентных уравнений и трудоемкость рекурсивных алгоритмов.

1.  T_n = T_{n -1} + C·n Þ T_n = O(n²).  (сортировка методом пузырька).

2.  T_n = 2T+ C·n Þ T_n = C·n·log n (быстрая сортировка, диаграммы Вороного).

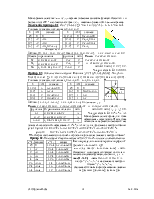
3.  T_n  £  c·n + и = a < 1, Þ T_n = O(n)  (k-ое число, МОД, ЛП в R²).

4.  T_n = T_{n -1} + C Þ T_n =  C·n (задача Штейнера).

5.  T_n = T_{n -1} + k·T_{n -2}. Решение ищется в виде T_n = lⁿ Þ lⁿ = l^{n –1} +k·l^{n -2}   или

l² = l + k Þ l_1,2 = ¹/₂ ±Þ , а C_1,2 зависят от T₁ и T₂

Таблица 1. Зависимость трудоемкости алгоритмов от размера задачи.