Стационарный режим процесса и его динамика. Скорость накопления промежуточного соединения. Теории катализа, страница 7

Разветвленные цепные р-ции(ц.р.) могут переходить во взрывной режим при определ-ных давлениях,тем-ре,составе реакцион. смеси и др. переменных. Экспер-но, на примере окис-я сероводорода кислородом,было установлено,что смесь может 3 раза переходить во взрывной режим,т.е. в смеси можно создать 3 значения давлений и тем-ры,при к-рых она взрывается.Эти дав-я и тем-ры наз-ют 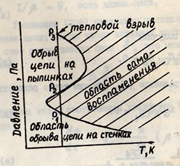пределами самовоспламенения смеси(см.рис.)При дав-ях ниже Р₁ смесь H₂S и O₂ не взрыв-ся,т.к. она значит-но разбавлена и среднее число актов обрыва цепей на стенках сосуда, в к-ром нах-ся смесь, превышает число разветвлений цепей.При Р₁ смесь взрыв-ся,т.к. в этом случае число обрывов цепи уже ниже числа развития цепей.При дав-ях выше Р₂ смесь не взрыв-ся,т.к. обрыв цепи происходит при столковении актив.частиц в объёме реакцион.смеси на пылинках(или др. массив.частицах).При дав-ях,равных Р₂, смесь взрыв-ся,т.к. число разветвлений цепей выше числа их обрывов на третьих частицах.3-ий предел взрыв-ти происходит при  Р₃ и обусловлен тепловой природой процессов,особ-но легко он проходит для экзотермич.р-ций.При сжатии смесей происходит их сильный разогрев,к-рый приводит к их взрыву.Тепловому взрыву способ-ют каталит.действи стенок сосуда,на к-рых при адсорбции могут создаваться актив.частицы.Особ-ть ц.р.- наличие периода индукции в превращении исх.смеси в-в.За время периода идукции в смеси накаплив-ся а.ч.,к-рые приводят к постепенному развитию ц.р. с послед. взрывом. . P₁,P₂,Р-предел.дав-я взрыва и общ.внеш.дав.Т₀-постоянная.При Р< P₁ и P> P₂ T₀<0→затух-щий пр-с,при P₁<Р< P₂ T₀>0→пр-с протекает с самоускорением.Т-хар-ет вр,в теч к-рого конц-я промеж. продуктов увел-ся в е раз. Вр,в теч. к-рого скорость пр-ся переходит от незначительной неизмер.вел. к оч.большой измер.величине.

53. Теория теплового взрыва.

Кратко рассмотрим анализ теплового режима в случае сильно экзотермической реакции.

В стационарном состоянии соблюдается тепловой баланс реакционной зоны, поскольку  тепловыделение за счет реакции и отвод тепла сбалансированы Q₊=Q_-. Для реакции 1го порядка можно записать

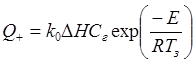   (4.10)

     (4.11)

где C_г – концентрация реагента в газовой фазе, a_t –коэффициент теплоотдачи, индексы ‘з’ и ‘о’ относятся к реакционной зоне  и окружающей среде. Ясно, что при низких температурах, когда наклон прямых теплоотдачи, т.е. a_t, больше, чем производная dQ₊/dT, реализуется стационарное состояние и т.д., вплоть до некой критической температуры T*, в которой a_t=dQ₊/dT, т.е. линия теплоотдачи становится касательной к кривой тепловыделения:

   (4.12)

Кроме того,  в точке Т = T* еще выполняется условие теплового баланса, т.е. Q₊ = Q_- Поскольку эта точка является переходной между кинетической и диффузионной областями, имеется также заметный градиент концентрации, и для  скорости реакции справедливо выражение

,   (4.13)

где k_m- коэффициент массопередачи. Используя известные из макрокинетики и теории подобия корреляции междуa_t  и k_m, в том числе числа Рейнольдса, Шмидта и Прандтля, найдем

k_m/a_t = 0,7/(c_p r),                                   (4.14)

где c_p и r означают молярную теплоемкость и плотность газообразной смеси. Окончательное выражение для критической температуры  T* имеет вид

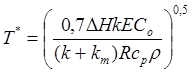.   (4.15)

Следует подчеркнуть, что при  температуре ≥T* стационарный режим в кинетической области уже невозможен, и система скачком (за время меньше 1 мин) переходит в диффузионную область, которая характеризуется весьма большим градиентом температуры DT= T_р –T_о. Этот самопроизвольный разогрев в реакционной зоне можно рассчитать в адиабатическом приближении, считая, что все тепло реакции идет на нагрев реакционной смеси. 

               (4.16)

33. Диффузионный скачок потенциала.

Для двух растворов с одинаковым растворителем, но разной концентраций, скачок потенциала на границе раздела бвух растворов наз-ся диффузионным. Скорости диффузии катионов и анионов различны. Раствор 2 получит избыток положительных, а 1- избыток отрицательных. С течением времени скорости становятся одинаковыми, в стационарном состоянии электролит диффундирует как единое целое. При этом каждый раствор имеет заряд, и разность поетнциалов между ними соответсвует диффузионному.