Если к двум несмешивающимся жидкостям добавить третий компонент, растворимый в обеих жид-ях, то он распределится между ними в определённом количественном соотношении. Это соотношение есть величина постоянная и называется термодинамическая коэффициентом распределения K:
При равновесии хим. Потенциал третьей жидкости в 2-х фазах будет одинаклов
μI3=μII3
Химический потенциалзависит от активности 3-го компонента в р-ре.
μ3 = μº3+ RT ln а3
μº(I)3+ RT ln а(I)3 = μº(II)3+ RT ln а(II)3
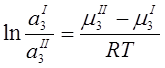
При Т=const
А3/а3 = с3/c3*y3/y3=K*y3/y3
Уравнение 
называется законом
распределения Нернста: распределение каждого из растворённых ве-в между двумя
фазами определяется коэф-ом распределения, величина кот-го не зависит от
присутствия других ве-в.
Коэф. распределения меняется с изменением конц. Распред-го вещ-ва в 2-х равновесных жидких фазах.
Важным следствием этого закона является экстрагирование, т.е. извлечение ве-ва из р-ра подходящим растворителем, который не смешивается с другим компонентом р-ра. С помощью экстракции можно разделять несколько веществ. Для увеличения полноты извлечения вещ-ва из водного слоя орг.растворителем экстрагирование проводят последовательно небольшими порциями экстрагента (υ), при этом чем больше число последовательных стадий извлечения (n), тем больше полнота извлечения при одном и том же кол-ве взятого экстрагента.
где V1-объем экстрагируемого раствора;V2-объем экстрагента; m0- масса компонента в исходной смеси и после первой экстракции осталось m1;
После n экстракций в первом растворе
останется вещества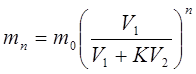 
24. Вывод уравнения, связывающего эквивалентную электропроводность с подвижностями ионов.
I. 
- электропроводность, где
ρ – удельное электрическое сопротивление
q – площадь электрода (далее поперечное сечение сосуда,[см2]
l – расстояние между электродами
χ – удельная электропроводность, [ом-1•см-1]
II. 
-
эквивалентная электропроводность, [см2/(г-экв•ом)]
где с – эквивалентная концентрация, [г-экв/л]
III. I = I++I- - количество электричества, перенесенное ионами через раствор в 1 сек
- количество катионов, прошедшее через поперечное
сечение за 1 сек
- сила тока, т.к. каждый г-экв ионов несет согласно
закону Фарадея F=96486 K эл-ва.
- скорость катионов, где u – абсолютная подвижность катионов, [см2/сек*в]
Аналогичные формулы для анионов (v, v’, c-, n-, I-)
Получаем:
IV. 
-
закон Ома
Подставим в это выр-е значение К из (I) и (II), и приравняв правые части уравнений (III) и (IV), получим
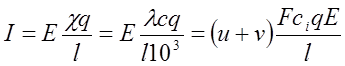
Решив уравнение относительно λ, получим
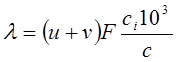
для сильных электролитов, диссоциация которых считается полной, отношение 103сi/с=1
для слабых - 103сi/с=α
V. Учитывая подвижности катионов и анионов,
V=v*F и U=u*F
получаем заданное выражение для разной степени диссоциации электролитов.
21. Скорость движения иона и его подвижность (уд и экв эл-ть сама)
Скорость движения ионаопределяется силой, действующей на ион, кот. равна произведению заряда иона на градиент потенциала поля, и фактором R, харак-щим сопротивление среды, зависящей от T, природы иона и раств-ля υi=(e*zi/R)*( ∆U/l) - zi – заряд иона; l – расстояние м/у электродами; ∆U – разность потенциалов м/у электродами.
Подвижность ионов – кол-во электр-ва, переносящееся ионом.
Ii=ni*F (равно произв-нию общего кол-ва ионов на число Фарадея).
29. Понятия о ЭДС, скачках потенциалов, элементе и полуэлементе. Причина появления электродного потенциала.
Элемент – емкость,разделенная полупроницаемой перегородкой на 2 части.В каждом отделении-электрод и р-р электролита, соединенные мет. проводником.
Полуэлемент-отд.емкость с р-ром и эл-дом.
Скачок потенциала-наличие двух типов зарядов на границе раздела двух фаз у стенки электрода.
В элементе создается поток электричества за счет различия в знаках зарядов электродов и наличия скачков потенциалов на границе металл-раствор.Разность этих скачков называют ЭДС и ее можно замерять,включая в цепь источник тока с равной по величине, но обратной по направлению.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.