μ = (Ма + Мв)/Ма•Мв – функция молекулярных масс реагентов число столкновений молекул А и В в единицу времени Δt, в единичном цилиндре определяется выражением:
z0 = 5,01•δAB2 [RTμ] 0,5
Полное число соударений в единицу времени в единице реакционного пространства равно Z = z0•nAnB, где nA и nB число молекул реагентов в указанном пространстве.
Доля активных соударений
ε =![]() = exp(-E/RT)
= exp(-E/RT)
Доля активных соударений растет с температурой существенно быстрее, чем кинетическая энергия частиц.
расчетное выражение скорости реакции по теории АС:
r = 5,01CACBNA δAB2 [RTμ] 0,5·exp(-E/RT)
k = 5,01NA δAB2 [RTμ]0,5·exp(-E/RT)
согласно
уточненной теории АС скорость реакции определяется тремя факторами: стерическим
(f), энергетическим (ε) и
транспортным (Z) или r = f.ε. Z причем
![]()
Транспортный фактор Z определяет частоту соударений молекул реагентов, энергетический фактор ε учитывает долю молекул с энергией, необходимой для реакций, а стерический фактор учитывает долю молекул с надлежащей конфигурацией при соударении.
45. Классификация реакторов химических процессов. Понятие о времени контакта.
Типы реакторов, используемых в химических процессах, подразделяют по режиму движения реакционной среды (смешения и вытесения), по условиям теплообмена (адиабатные, изотермические, политропные),по способу подачи реагентов на периодический или статический (например, автоклав) и проточный, а по профилю концентраций и температур различают безградиентный (например, реактор идеального перемешивания) и реактор идеального вытеснения, который может быть дифференциальным (с малыми градиентами) и интегральным, в котором имеются значительные градиенты.
Время перехода из одного стационарного режима в другой обычно называется временем релаксации системы.
Общее выражения для расчета времени контакта для получения заданной степени превращения в реакторе идеального вытеснения:
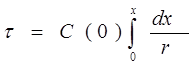
46. Кинетика гомогенных необратимых реакций, протекающих в условиях идеального перемешивания и идеального вытеснения.
А) На основеобщего выражения для расчета времени контакта для получения заданной степени превращения в реакторе идеального вытеснения:
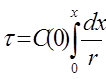 (79)
(79)
рассмотрим реакцию 1-го порядка, протекающую с изменением числа молей:
А ® В + D
и выразим концентрацию реагента через конверсию:
![]() (82)
(82)
((1+x) в знаменателе появляется из-за увеличения числа молей в реакционной смеси по мере протекания реакции). Подставляя (82) в выражение скорости реакции, возьмем интеграл (79), который в этом случае имеет вид:
k.t = -2ln(1-х) – х (83)
б) Реактор идеального перемешивания является безградиентным, т.е. скорость процесса в реакторе не зависит от тепло- и массопереноса, геометрии реактора, скорости потока и др. макроскопических параметров. В таком реакторе расчеты существенно упрощаются по причине отсутствия градиентов концентраций – следовательно, не надо интегрировать дифференциальные уравнения. Запишем уравнение материального баланса по исходному веществу А
QA(C0 – CA) – rVR = 0 (84)
или вводя время пребывания в реакторе
C0 – CA = τ.rA (85)
Разделив (85) на C0, получим
x = τ rA/C0 или τ = x C0 / rA (86)
В таком реакторе расчеты существенно упрощаются по причине отсутствия градиентов концентраций – следовательно, не надо интегрировать дифференциальные уравнения. Запишем уравнение материального баланса по исходному веществу А
QA(C0 – CA) – rVR = 0 (84)
или вводя время пребывания в реакторе
C0 – CA = τ.rA (85)
Разделив (85) на C0, получим
x = τ rA/C0 или τ = x C0 / rA (86)
51. Примеры вывода кинетических уравнений цепных реакций в стационарном приближении.
Можно описать в стационарном приближении кинетику неразветвленной цепной реакции на примере цепной реакции разложения ацетальдегида с образованием метана и монооксида углерода в качестве основных продуктов
СН3СНО à СН4 + СО (4.R1)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.