Финитные регуляторы и их свойств. Материалы по процедурам модифицированного метода динамического синтеза дискретных САУ, страница 9

.                                  (8. 14)

Аналогичным образом преобразована и ДПФ цифрового регулятора.

                                                            (9. 14)

Отметим, что в ДПФ компенсационного последовательно - включенного регулятора полином нулей принимается равным полиному полюсов ДПФ объекта C(z^-1)=A(z^-1)

Теперь, согласно работе [¹⁾], запишем ДПФ структуры системы, изображенной на рис 7.14.

                                                    (10. 14)

Расчеты по формуле (10. 14) выполняются при нулевых начальных условиях, поэтому принимают b0 = 0.

Если , то из первой формулы (10. 14) найдем:

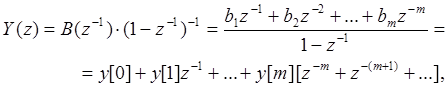                                 (11.14)

где у[i] - значения решетчатых функций на выходе замкнутой ДСАУ, причем у[0] = 0 и у[m] = 1, a^!0 = 1 и a^!1 = -1.

В самом деле, деля полином числителя на полином знаменателя в выражении (11.14), получим:

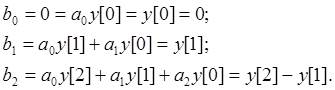             (12.14.)

Соответственно:

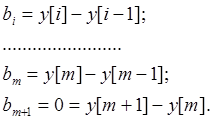
Откуда

    и т.д.

Таким образом, выбирая ДПФ F(z) согласно выражению (10.14), получаем на "m "интервалах апериодический переходныйпроцесс в ДСАУ.

Можно рассчитать и значения переходной функции u[i] на входе УМ (рис. 6. 14 и рис. 7. 14), т. е. на выходе регулятора. Тогда оперируем со второй формулой (10.14).

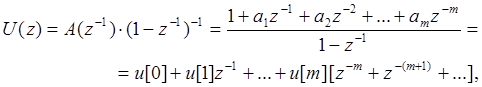
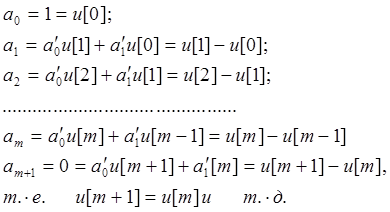                                      (13. 14)

Если обозначить:

,                                (14. 14)

(напомним, что финитный переходный процесс проходит при нулевых начальных условиях, поэтому =0), а ДПФ по выходу U(z) принять:

.                      (15. 14)

Тогда получим:

 и .                                                (16. 14)

Следовательно, первое выражение (16. 14) позволяет рассчитать коэффициенты pi и qi, зная обобщенные параметры объекта ai и bi, а второе - определяет вид ДПФ, параметры ФЦР и алгоритм его реализации. Исходя из условий (14. 14) - (16. 14), получим основную расчетную формулу для модели объекта ФДСАУ.

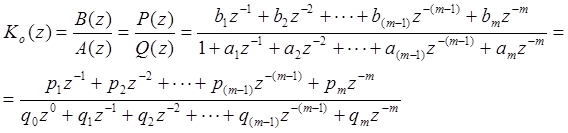                            (17. 14)

Поделив все слагаемые полиномов P(z) и Q(z) на , найдем такие соотношения для параметров и коэффициентов:

                                                         (18. 14)

          Таким образом, мы установили взаимосвязь коэффициентов pi и qi, и обобщенных параметров объекта ai и bi. Формулы (18. 14), совместно с уравнениями (12. 14) и (13. 14), позволяют установить и другие полезные и необходимые сведения.

Из систем уравнений (12.14) и (18. 14) установим:

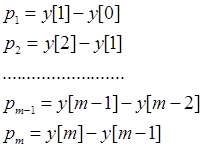
Учитывая то, что y[0]=0, получим следующую зависимость:

                                                                                                     (19. 14)

          Аналогично можно поступить системами уравнений (13. 14) и (18. 14):

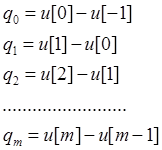                                                                                (20. 14)

Просуммируем коэффициенты полинома Q(z):

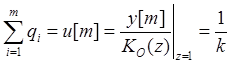                     +.                                              (21. 14)^*)

Осталось определить значение коэффициента :

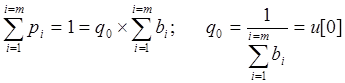                                                        (22. 14)

Теперь определим взаимосвязь параметров оптимального дискретного регулятора и объекта при финитном апериодическом управлении, рассчитанном по методике Джури и Шредера.

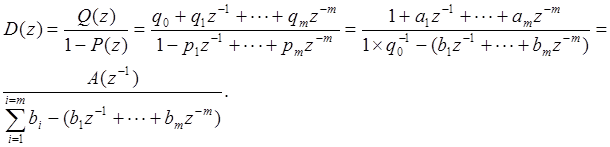  (23. 14)

            Итак, соотношение (23. 14), в принципе, важно тем, что, зная параметры объекта, можно сразу же определить структуру и параметры оптимального финитного апериодического регулятора.

_____________________________________________________________________________

^*) Это напоминание для тех студентов, которые так и не усвоили важность для повседной инженерной деятельности понимание сути простейшей теоремы "О начальном и конечном значениях функций" и не освоили умение её использовать. Я в курсе "Теория управления" уже показал не меньше сотни примеров полезности её применения, и в материалах этой лекции пользовался этой теоремой неоднократно. Что касается утверждения о плохом усвоении сути теоремы частью студентов? Это мнение складывается из анализа ответов на четырех (!!!) экзаменов по учебной дисциплине "Теория управления", просмотр части отчетов студентов по различным практическим работам и анализе докладов выпускников кафедры на ГЭК"ах" и ГАК"ах". Методических упущений по этому вопросу в курсе я не вижу. Поэтому готов выслушать и принять, с благодарностью, любые разумные советы и предложения (С. Ковчин).