Финитные регуляторы и их свойств. Материалы по процедурам модифицированного метода динамического синтеза дискретных САУ, страница 7

Разрешить выражение (4.14) теперь возможно, применяя способ наименьших квадратов к выражению (5.14) и определяя производные , где s = 1, 2, 3... (n-m).

По существу, второе слагаемое КСО (4.14) характеризует затраты энергии системы, т.е. минимизирует потери в ФДСАУ на регулирование, первое слагаемое характеризует систему оптимального быстродействия. Варьируя значения l и x, можно придавать функционалу (4.14) разные свойства.

Второй метод оптимизации связан с ограничением мощности ДСАУ, т.е. ограничением величины U[i] на выходе УМ:

.

Очевидно, величина uмакс должна задаваться перед выполнением расчетов ФДСАУ.

Третий метод оптимизации обеспечивает получение субоптимального регулятора нечувствительного к вариациям параметров. Для этого используется следующая КСО:

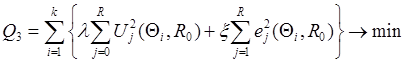, где Q0 - вектор состояния ДСАУ с образцовыми (базовыми) значениями параметров; R0 - структура субоптимального регулятора при базовых параметрах модели; Qi - вектор состояния системы при вариациях параметров от i = 1 до k.

Результаты использования всех трех методик оптимизации параметров финитного регулятора были проверены на конкретных системах. Эти исследования показали, что при 50% вариациях параметров объекта второго прядка k, Т₁, Т₂ коэффициенты субоптимального управления c1 и c2 [см. выражения (4.14) и (5.14)] изменились первый, не более, чем на 1,5%, а второй - до 0,3%. Следовательно, принятый алгоритм расчета финитного регулятора обеспечивает малую чувствительность коэффициентов субоптимальности ci к вариациям параметров объекта управления. Но это еще не гарантирует инвариантность характеристик процессов управления к этим вариациям. Переходный процесс ФДСУ в этом случае имеет колебательный характер.

Вторая методика была применена к исследованию управления минимально-фазным объектам третьего порядка. При таком субоптимальном законе управления и ограничении выхода усилителя мощности величиной uмакс все дальнейшие значения u[i]<uмакс. Зависимости y[i] при оптимальном и субоптимальном апериодическом управлении существенно отличаются величиной перерегулирования.

Значительное число работ, принадлежит научной школе Дрезденского Технического Университета (ДТУ), где выполнены многие исследования данной проблемы с использованием полиномиального принцип выбора структуры и параметров финитного апериодического регулятора(А.Бергена и Дж. Рагаццини¹⁾). Подробное изложение результатов научной школы ДТУ, и их доскональный анализ содержатся в работе [¹⁶⁾], на которую мы будем неоднократно ссылаться.

В 90 - е годы XX века в этом направлении активно работала  научная  школа кафедры САУ СПбГПУ. Вопросы финитного управления металлорежущими станками составили часть докторской диссертации О. А. Соколова. Под руководством доктора техн.наук, профессора О.А. Соколова и автора этих лекций по отдельным аспектам проблемы финитного управления были выполнены многочисленные научные исследования. Успешно защищены кандидатские диссертации, А. Н. Беляевым,(погибшим в автокатастрофе )талантливым молодым ученым - инженером, А.Г.Злобиным, Шати - Абдерразаком -Бен - Нажи (Тунис), Абделем.Керимом Хаммами (Тунис). А сколько еще интересных исследований осталось не завершенными в это трудное для России время!

________________________________________________________________________________

¹⁵⁾ Janiszowski K. Verallgeinerter Dead-beat Regler// MSR, 1982, H.2, S. 70-74.

¹⁶⁾ Хаммами А.К. Разработка методологии, расчет и исследование финитных электромеханических систем с цифровым управлением. Диссертация на соискание учёной степени кандидата техн. наук СПб, СПБГТУ, 1998

10. 2. 3. Современное состояние проблемы конструирования финитных регуляторов для управления техническими объектами

На основании анализа всех материалов данной главы, которые полностью заимствованы из работы [¹⁶⁾] представлены решения различных аспектов проблемы и их хронологию в виде рис.4. 14. Итак, работы 30...50-х годов являлись основанием для появления разработок основополагающих идей в области финитного автоматического управления, которые были выполнены в 50-е годы. Интенсивное развитие теоретических разработок этих основополагающих идей было проведено в 70 - .80-е годы. Подводя итоги описания, изложенного в разделах 10. 2. 1 - 10 2. 2., можно резюмировать следующее: