Финитные регуляторы и их свойств. Материалы по процедурам модифицированного метода динамического синтеза дискретных САУ, страница 4

Первые работы по использованию КСО принадлежат С. Чангу [^6),7)] (США), а так же Л. Волгину и Л. Смоляру (Россия) [^8),9)]. Результаты этих основополагающих разработок удачно обобщены Я. Цыпкиным (Россия) [3]. Сущность их состоит в нижеследующем.

Пусть yо[n,0] заданная решетчатая переходная характеристика оптимальной замкнутой ДСАУ с известным сигналом управления g[n,0], а y[n,0] - аналогичная характеристика исследуемой системы. Тогда получим:

.                                       (2.14)

В выражении (2.14) y[n,0] реакция на такой же сигнал замкнутой ДСАУ, содержащей объект с известной ДПФ и любую коррекцию в виде последовательного, параллельного устройства или в виде обратной связи. Все эти дискретные коррекции подробно изучены в работе [3.]. Будем считать, что в дальнейшем мы пользуемся последовательной коррекцией с неизвестной ДПФ - D(z) ( рис.5.14). Тогда можно записать:

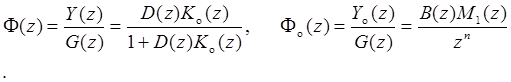                            (3.14)

Для финитных ДСАУ используют не бесконечный верхний предел суммы (3.10), а конечный n = m + k, где m - порядок известного полинома знаменателя ДПФ модели объекта K_o(z) = В(z)A(z)-1, а k число дополнительных интервалов субоптимального управления.

Таким образом, в выражении Ф₀(z)отражены условия сохранения в модели оптимальной ДСАУ полинома числителя модели объекта и полинома М₁(z) "субоптимальности". Теперь можно перейти к таким выражениям:

Далее, возможно исследовать выражение (3.13) на минимум с помощью дискретной формулы Парсеваля-Релея и рассчитать параметры ДПФ коррекции D(z).

Э.Джури в работе [1] предлагает несколько иную методику использования КСО для расчета финитных ДСАУ. Однако минимизация любых КСО приводит к сложным аналитическим исследованиям, что будет показано ниже. Это является недостатком метода.

Итак, подводя итоги работ, выполненных в 50-е годы, можно сделать такие выводы.

1. Выдвинуты два критерия создания финитных ДСАУ. Линейная суммарная оценка (ЛСО) используется для построения финитных систем с апериодическими переходными процессами, КСО применяют при реализации ФДСАУ с минимальной квадратичной ошибкой рассогласования реального и оптимального дискретных процессов.

2. Сформулированы два метода использования ЛСО для расчета финитных апериодических цифровых регуляторов, первый из которых базируется на задании типовых полиномов ДПФ модели разомкнутой (замкнутой) финитной ДСАУ при известных сигналах управления, а второй обеспечивает характер финитного дискретного апериодического процесса при любом виде ДПФ модели объекта Kо(z), но при сохранении в ДПФ модели финитной замкнутой системы полинома числителя объекта управления.

3. Определены основные недостатки финитных ДСАУ:

- возможность значительного перерегулирования в межтактовые периоды;

- возможность подачи неоправданно больших форсировок сигнала на объект управления.

4. Не получены, при использовании ЛСО, законы субоптимального финитного апериодического управления. Практически не решены технические задачи реализации финитных ДСАУ. Не исследованы влияния вариаций параметров ДСАУ и интервалов квантования на характеристики финитных процессов. Четко не сформулировано понятие "финитного дискретного апериодического процесса".

Например, огибающая h₁[nT], изображенная на рис. 1.14 в виде ломаной линии является идеальной характеристикой финитного апериодического дискретного переходного процесса при m = 4. Но такому же определению финитного апериодического дискретного переходного процесса отвечает и кривая h₂[nT], которая более соответствует физическому процессу в реальном объекте. В самом деле, если - угловая скорость объекта в ЭМС, то в точке излома при m = 4, (двигаясь по ломаной h₁[nT]) неопределенным становиться угловое ускорение , точнее оно мгновенно изменяется от до.Физически такой динамически процесс невозможен. Поэтому действительное изменение h(t)происходит не в виде ломаной, а в форме кривой h₂[nT]. Причем эта кривая не отвечает признаку апериодичности, принятому в теории автоматического управления для аналоговых систем. Следовательно, в реальных САУ действительный переходный процесс является колебательным затухающим. Финитный же апериодический дискретный переходный процесс есть только расчетный процесс в математической модели ДСАУ, который достигается при межтактовых отклонениях выходной координаты системы, не превышающих заданную трубку точности, в установившемся режиме движеия при nT≥mT..