1. До сих пор четко не сформулировано понятие финитного дискретного апериодического процесса, что затрудняет проведение теоретических исследований задач финитного управления.
2. Все методики расчета параметров субоптимального управления, использующие КСО, сложны, а значения весовых коэффициентов слагаемых минимизируемого функционала качества оказываются неопределенными.
3. Не решена проблема создания финитных ДСАУ малочувствительных к вариациям параметров и возмущений.
4. Практически не решена задача выбора величины интервала квантования в финитных ДСАУ. Все рекомендации базируются на исследованиях Р. Изермана [29](ФРГ) или работах О. А. Соколова для приводов станков с ЧПУ (Россия). Все они носят частный характер.
5. Работы 80 -х годов сосредоточены на исследовании математических информационных моделей финитных ДСАУ. Попытки учета в них характеристик реальных технических объектов малочисленны и не всегда корректны [например,17)].
6. Совершенно отсутствуют методики учета энергетических ограничений, которые накладываются на финитные процессы управления реальными параметрами и характеристиками элементов технических объектов управления.
7. Совершенно не изучались возможности использования других экстраполяторов дискретных сигналов при финитном управлении, кроме нулевых.
8. Слабо изучены вопросы поведения финитных ДСАУ в межтактовых интервалах.
Это резюме уточняет состояние проблемы финитного управления к началу 90 - х годов и конкретизирует бόльшую часть научных задач, которые были более или менее успешно решены в 90-е годы XX века и первое десятилетие XXI века в научной школе СПбГТУ.и других научных школах..
______________________________________________________________________________-17) Geitner G.H., Stoev A. Optimiert auf endliche Einstellzeit. Teil I// MSR, N28, 1985 (2) - S.60-68; Teil II// MSR, N28, 1985 (4) - S. 165-169.
10. 3. Методика расчета (конструирования) оптимальных и субоптимальных финитных апериодических регуляторов для управления элктромеханическими системами
10. 3. 1. Вводные замечания
Первое упоминание dead-beat controller было использовано Э. Джури (США) в основополагающей работе1) по создания оптимальных по быстродействию "финитных апериодических регуляторов". Напомним, что идея таких регуляторов родилась в 50-е годы ХХ века, но тогда их невозможно было практически реализовать (также как и системы подчиненного управления, в то же время предложенные Кесслером). Реализация ФДСАУ стала возможной в 80-е годы, когда появилась «нормальная» электроника. По финитным регуляторам на кафедре САУ были выполнено много исследований, о которых указано ранее.
По мнению профессора Ковчина путь решения задачи, изложенный в работе [2)] является «тупиковым», так - как мы заранее ограничиваемся количеством структур моделей объекта. Поэтому воспользуемся методикой Джури и Шредера [1)].
На рис 6. 14 изображена функциональная схема исследуемой системы,
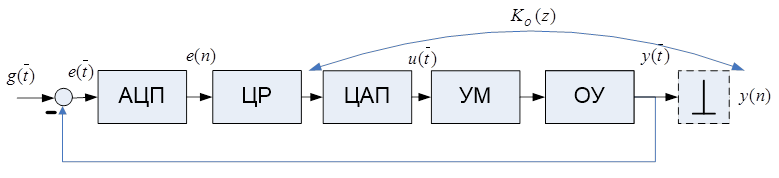
Рис.6. 14 . Функциональная схема системы.
Здесь принято: ЦР – цифровой апериодический регулятор, УМ – усилитель мощности, ОУ – объект управления. Объект включает - экстраполятор нулевого порядка (ЦАП), УМ и ОУ. Теперь непосредственно рассмотрим структурную схему системы управления (рис. 7. 14)
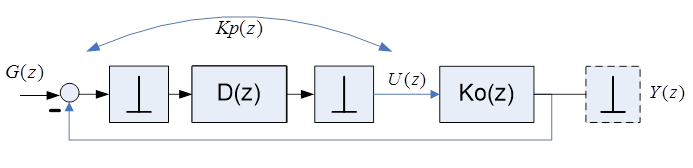
Рис.7. 14. Структурная схема системы.
Пусть дискретная передаточная функция (ДПФ) объекта Ko(z)представлена в таком виде:
, (6.
14)
где 
и порядок "k" полинома B(z) меньше порядка "m" полинома A(z).
Далее, обеспечивая для реализации финитного апериодического управления k = (m-1),поделим полиномы числителя и знаменателя ДПФ Ko(z) на zm и получим:
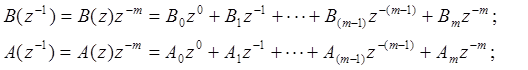(7.14)
Для дальнейшего упрощения записи Ko(z) слагаемые обоих полиномов (7. 14) поделим на A0. Тогда выражение (6.14) примет такой вид:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.