Первыми работами, где были предложены (ЛСО) для конструирования ФЦР, были [2)] и [1)]. В работе [2)] А.Бергена и Дж.Рагаццини впервые поставлена и решена задача получения конечного времени апериодического переходного процесса в ДСАУ.
____________________________________________________________________
3) Фельдбаум А.А. Основы теории оптимальных автоматических систем.- М.: Физматгиз, 1963.- 552 с.
4) Лернер А.Я. Принципы построения быстродействующих следящих систем и регуляторов.- М.: Госэнергоиздат, 1961.
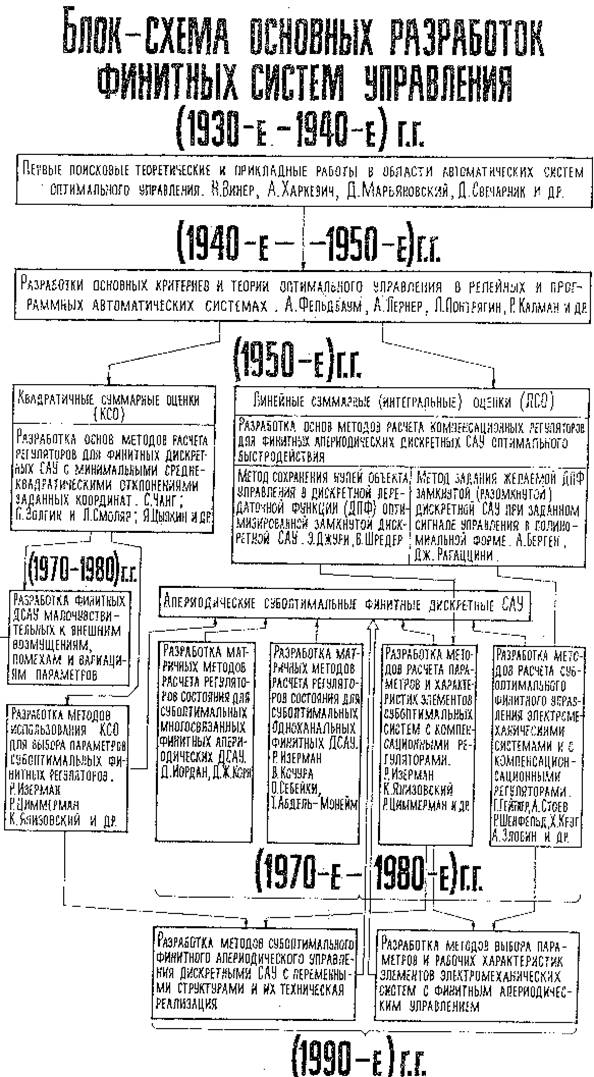
Рис4.14
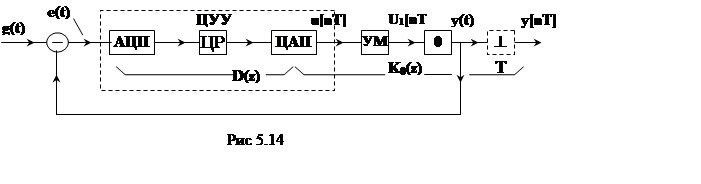
При этом было рассмотрено поведение ДСАУ (см. рис.1. 14 и рис.5. 14) при входных сигналах вида: g(t) = 1(t), g(t) = kvt*1(t), g(t)=ka2*1(t). Для этих сигналов приведены типовые передаточные функции разомкнутых дискретных САУ K(z), которые сведены в табл.3.14:
K(z) = D(z)×Kо(z) , (1.14)
где D(z) - ДПФ финитного ЦР, Kо(z) -ДПФ аналогового объекта управления с экстраполятором нулевого порядка. Зная Kо(z) и ДПФ K(z), легко получить и выражение D(z). В той же работе впервые исследуются финитные ДСАУ, содержащие элементы чистого запаздывания.
Здесь же впервые поставлен вопрос о необходимости ограничения форсировки сигналов u(t) на входе объекта управления при финитном управлении. Таким образом, в этой (первой) работе предложен метод использования типовых полиномов для конструирования финитных апериодических ДСАУ. В табл. 3.14, частично заимствованной из [2)], представлен ряд типовых полиномов разомкнутых ДСАУ, отвечающих структуре рис. 5.14.
 |
Следует обратить внимание на обозначения аргументов в формуле (1. 14)
![]() , где B(z)= b0zm+b1zm-1+...+bm; A(z)= a0zn+a1zn-1+...+an.
, где B(z)= b0zm+b1zm-1+...+bm; A(z)= a0zn+a1zn-1+...+an.
Но B(z-1)= B(z)z-n= b0zm-n+b1z(m-1)-n+...+bmz0-n; A(z-1)= A(z)z-n= a0+a1z-1+...+an z-n.
Например, для ДСАУ с
моделью второго порядка (m=2) при g[nT}=1[nT] имеем:
![]() .Зная Ko(z-1),
найдем D(z-1)=K(z-1)/K0(z-1).
.Зная Ko(z-1),
найдем D(z-1)=K(z-1)/K0(z-1).
Недостаток этого метода связан с ограничеием функций Ko(z-1),
В работе [1)] Э.Джури и В.Шредера представлен иной, более общий подход к конструированию "апериодического финитного ЦР" (Dead-вeat controller). Этот термин впервые применен ими. К сожалению, далеко не всегда он получил в отечественной литературе надлежащий перевод (например, встречается "русифицированный" термин "дит-бит регулятор").
Подробное изложение этого метода дано в разделе 10. 3.
Попутно отметим, что термин "финитный" (т.е. заранее численно ограниченный по времени) процесс был введен в России в 60 е годы XX века Ф.Г. Бутковским5) и это понятие распространено далее на регуляторы и системы.
Применение ЛИО в качестве базового критерия вполне оправдано теоретически для конструирования ФДСАУ по методикам Бергена или Джури, поскольку в них реализуются "апериодические" переходные процессы.
Перейдем теперь к изложению второго метода конструирования ФДСАУ, критерием которого служат квадратичные суммарные оценки (КСО) (см. рис 4.14).
_____________________________________________________________________________
5)Бутковский А.Г., Полтавский Л.Н. Некоторые задачи обобщенного и оптимального финитного управления линейными системами с сосредоточенными параметрами// Автоматика и телемеханика, 1967, N10,c. 32-40.
Таблица 3.14
Характеристики финитных дискретных систем автоматического управления
|
Значение ДПФ F(z) |
Значение ДПФ D(z)×Kо(z) |
при g[n]=1[n] |
|
z -1 |
z-1(1-z-1)-1 |
(1-z -1) -1 |
|
z -2 |
z -2(1-z -2) -1 |
(1-z -1) -1 |
|
z -3 |
z -3(1-z -3) -1 |
(1-z -1) -1 |
|
z -m |
z -m (1-z -m) -1 |
(1-z -1) -1 |
|
2z -1-z-2-a |
a[(1-z -1)2] -1 |
g[n]=kvn |
|
3z -2-2z -3-b |
b[(1-z -1)2(1+2z -1)] -1 |
|
|
4z -3-3z -4-c |
c[(1-z -1)2(1+2z -1+3z -2)] -1 |
"-" |
|
5z -4-4z -5-d |
d[(1-z -1)2(1+2z -1+3z -2+4z -3)] -1 |
"-" |
|
mz -(m-1)-(m-1)z -m-h |
h[(1-z -1)2(1+2z -1+3z -2+4z -3+... ...+(m-1)z -(m-2))] -1 |
"-" |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.