Подавляющее большинство указанных выше публикаций посвящено описанию теоретических задач и методов их решения. Содержание немецких источников более направлено на решение практических задач использования финитного управления для автоматизации технических систем и объектов. Из этого цикла отметим работу [14)] Р. Циммермана. В первой ее части изложена методика расчета апериодического оптимального и субоптимального финитного ЦР, не отличающаяся от методики, использованной в работе [29].
_____________________________________________________________________________
10) Isermann R., Kurz H. Parameteradaptive Regelalgorithmen mit reversiven Parameter schatz verfahren /Regelungstechnik. 1979, H.// S.341-348.
11) Kucera V. The Structure and Properties of Time-Optimal Discrete Linear Control/ IEEE. Trans. on Automatic Control. Vol. AC-16, N4. 1971. p.p. 375-377.
12) Sebakhy O.A, Abdel-Moneim T.M. Design of Optimal Dead-Beat Controllers/ IEEE Trans. on Automatic Control. Vol. AC-25, N3, 1980, p.p. 604-606.
13) Jordan D., Korn I. Deadbeat Algorithms for Multivariable Process Control/ IEEE Trans. on Automatic Control Vol. AC-25, N3, 1980. p.p. 486-491.
14) Zimmerman R. Dead-beat Regelalgorithmmen fur Mikroprozessor-Regler// MSR N23, 1980, H.2,-S.-68-72.
Но, если в монографии [29] описаны субоптимальны ФДСАУ с числом дополнительных шагов k=1, то в работе [14)] изложена методика расчета таких систем с неограниченным числом S=k. При этом использовать выражение ДПФ объекта (см. рис.5.14) в таком виде:
, где
d - относительное время чистого запаздывания t/T,
и Т - период квантования.
Коэффициенты дополнительного полинома L(z-1) (в оригинале "Zusatzpolinom") могут быть найдены в результате задания значений выходных координат регулятора u(i). Однако выполнение этой процедуры нам представилось сложным. Наконец, в работе [14)] повторены те же рекомендации по выбору величины "Т", что и в [29]. С пригодностью этих рекомендаций для любых финитных ДСАУ трудно согласиться. Ценность же работы [14)] состоит в том, что в ней предложены три методики определения коэффициентов дополнительного полинома L(z-1).Описание этих методик здесь не приводится.
В работе К.Янизовского [15)] по существу рассматривались те же вопросы. В первой ее части описаны общие подходы к решению задач апериодического оптимального и субоптимального управления, которые повторяют изложение работ [29] и [14)]. Однако следует подчеркнуть, что здесь четко сформулированы и основные недостатки финитного управления, к главным из которых относятся следующие:
- вероятность больших отклонений выхода ДСАУ в установившемся режиме работы;
- большая величина перерегулирования при оптимальном финитном управлении;.
- высокая чувствительность параметров регулятора к вариациям параметров объекта.
Во второй части статьи предложены три метода выбора параметров субоптимального финитного управления ("Вestimmte Einstellzeit" - BEZ). Все три метода базируются на использовании КСО. В этом смысле данная публикация солидаризируется с работами [3.-8) 9)].
Следовательно, практически одновременно произошло использование метода квадратичной интегральной оценки для решения различных прикладных задач финитного управления несколькими авторами (в США, Египте, Германии, России). Это обусловлено тем, что к концу 70-х годов метод КИО был детально разработан теоретически и инструментально, в смысле создания алгоритмов его применения для решения различных прикладных задач.
Первый метод оптимизации К.Янизовский увязал с оценкой выходной координаты регулятора и переходной функцией ФДСАУ. При этом используется КСО в таком виде:
, (4.14)
где 
; n=m+k; l³0; x³0.
Если в формуле (4.14)
сделать подстановки:
при b0=0 и с0=1, 
при a0=1, то она примет
такой вид:
, (5.14)
где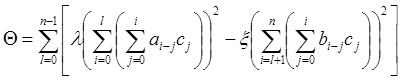 
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.