Практически реализовать оптимальный финитный регулятор невозможно, так - как порядок моделей реальных устройств ЭМС мал*). Приходиться использовать субоптимальный финитный регулятор с количеством тактов квантования не "m", а (m+k).
Субоптимальные регуляторы удобно применять в системах подчиненного управления (СПУ), так - как в каждом контуре удобно (и физически ясно) как выбрать ограничения. Напомним структуру типовой СПУ для ЭМС:
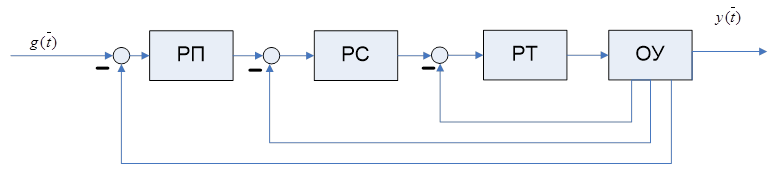
Рис. 8. 14. Функциональная схема типовой СПУ для ЭМС.
Здесь принято: РТ - регулятор тока, РС - регулятор скорости, РП - регулятор положения, ОУ - объект управления (усилитель мощности, электродвигатель, преобразователь механических движений (координат) (редуктор) рабочие органы исполнительного механизма**) и датчики - преобразователи координат управления: тока двигателя, скорости вращения вала
_____________________________________________________________________________
*) Например, в реальных микроконтроллерных устройствах управления время квантования исчисляется в миллисекундами, а порядок физичских моделей ЭМС "m"= (2 - 5). Поэтому, если реализовать финитный регулятор, скажем, в контура управления током двигателя, то (при компенсации постоянной времени якорной цепи) потребовалась бы для разгона и торможения огромная форсировка тока двигателя. Как следствие потребовался бы УМ в десятки (если не сотни) раз мощнее двигателя, со всеми вытекающими отсюда последствиями и со сгоревшим двигателем.
**) Термин "исполнительный механизм" подразумевает самые разнообразные по назначению устройства. Это и однокоордиатный сверлильный станок ("дрель") и многокоординатный металлообрабатывающий станок с ЧПУ, или промышленный робот с взаимосвязанными системами управления коордннатными приводами, бумагоделательная машина, или прокатный стан длиной в сотни метров с десятками взаимосвязанных ЭМС и верхним уровнем иерархии автоматического управления всем технологическим процессом изготовления бумаги или разнообразного проката металла.
механизма и его перемещения). Таким образом, приходится "очень уважительно" относиться к составлению математической модели ОУ
В СПУ вводятся реальные ограничения на её координаты, которые несут сведения об энергетике элементов ОУ (т.е. РТ), а не о преобразованиях информации как в РП и РС.
Для субоптимальных регуляторов справедливы соотношения:
![]() ,
,
![]() ,
,
где k – количество
дополнительных интервалов квантования переходного процесса, необходимых для
соблюдения заданных (задаваемых в процессе расчета) энергетических ограничений.
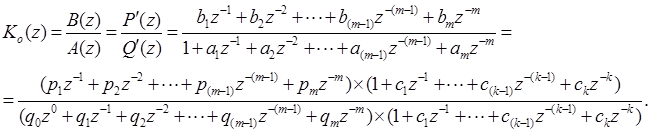 (24. 14)1
(24. 14)1
Выражение (24. 14)1 необходимо представить в иной форме, а именно:
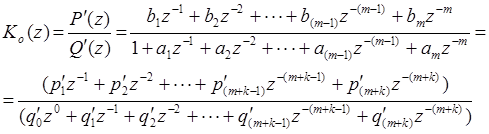 .
(24. 14)
.
(24. 14)
Взаимосвязь
коэффициентов p!i q!i
и
параметров объекта управления ai bi устанавливается
следующими соотошениями:![]() при b0=0 и c0=1,
при b0=0 и c0=1, ![]() при a0=1, а при j>k, все cj=0.
при a0=1, а при j>k, все cj=0.
Для нахождения коэффициентов ci необходимо воспользоваться следующими выражениями:
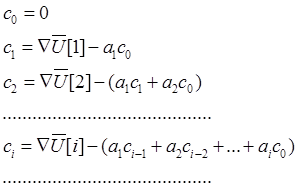 ,
(25. 14)
,
(25. 14)
где ![]() .
.
Теперь можно определить и ДПФ субоптимального регулятора:
![]() ,
,
Перечислим основные ограничения для реализации субоптимальных регуляторов
1. Ограничение по параметрам усилителя мощности.
Необходимо выполнить условия:
![]() .
.
Кроме того, должно соблюдаться неравенство:
![]()
где M , k – параметры УМ:
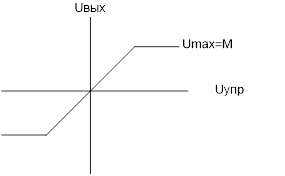
Рис.9. 14 Статическая характеристика УМ.
![]() ; динамическая
характеристика УМ
; динамическая
характеристика УМ ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.