Процедуры модифицированного метода динамического синтеза для ИС и ЦАС. Расчётная математическая модель аналого-дискретно-аналоговой электромеханической системы

Лекция 13. проф.

ГЛАВА 9. Синтез ДСАУ

Содержание лекции 12. Изложены процедуры модифицированного метода динамического синтеза для ИС и ЦАС. Представлены вспомогательные материалы (таблицы показателей качества), необходимые для выполнения инженерных расчетов коррекций в таких системах.

9. 5. Синтез Аналого-цифро-аналоговых систем (АЦАС)

.

9. 5. 1. Расчётная математическая модель аналого-дискретно-аналоговой электромеханической системы

Известно, что основным дискретным элементом в ЭМС является усилитель мощности (УМ). Поэтому её расчетная модель представляет собою не линейную цифро-аналоговую систему (ЦАС) (как полагают многие), а нелинейную аналого-дискретно-аналоговую (АДАС). Синтез АДАС практически не решен, что и определило необходимость этих исследований. В этом разделе представлены расчётные модели для структурно-параметрического синтеза компенсационных регуляторов для таких систем.

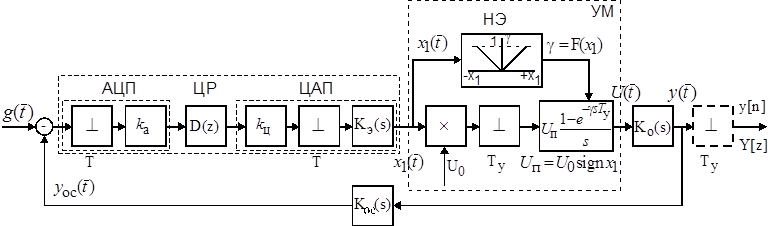
Рис.1.13 Структурная схема электромеханической системы с цифровым управлением

В состав типовой модели ЭМС постоянного тока с цифровым управлением (рис.1.13) входят: цифровой регулятор (ЦР) с дискретной передаточной функцией (ДПФ) D(z), программно реализующей коррекцию системы; усилитель мощности (УМ), формирующий импульсы выходного напряжения U() с периодом коммутации T_у; непрерывный объект управления (ОУ) с передаточной функцией (ПФ) K_o(s) и датчик сигнала обратной связи с ПФ K_ос(s).

Цифровой регулятор имеет линеаризованные модели аналого-цифрового и цифро-аналогового преобразователей (АЦП) и (ЦАП) с импульсными элементами, квантующими информацию с периодом T и модель вычислительного устройства, программно реализующего ДПФ D(z). Коэффициенты передачи АЦП и ЦАП соответственно приняты: k_A=1/d_A и k_ц=d_ц/1, где d_Aи d_ц - кванты аналогового и цифрового сигналов этих преобразователей. На выходе модели ЦАП имеется  экстраполятор с ПФ K_Э(s). Обычно преобразователи подбираются так, чтобы d_A= d_ц, тогда k_Ak_ц=1. Поскольку в реальных устройствах T << T_у, то дискретностью ЦР пренебрегаем. Тогда дискретную модель ЦР заменяем аналоговой с ПФ D(s).

Усилитель мощности включает в себя нелинейный блок умножения напряжения U_о(t) и знака сигнала sign x₁(), а также ключ с периодом коммутации T_у, на выходе которого формируется импульсный сигнал U_П[n]= U_о sign x₁. Нелинейный элемент (НЭ) преобразует сигнал x₁(), в относительную ширину g импульсного напряжения U()  выхода формирователя. Таким образом, расчётная модель УМ сохраняет свойства дискретной динамической нелинейности.

Часто модель датчика обратной связи представляет собою апериодическое звено с малой постоянной времени T_ос  и с ПФ такого вида: K_ос(s)= k_д( 1 +T_ос s )^-1» k_д. Далее для упрощения решений принимаем K_ос(s)» k_д.

9.5. 2. Структурная схема расчётной модели АЦАС

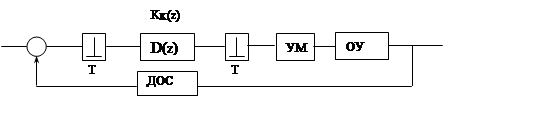
Рис.2. 13.

На рис.2. 13 изображена упрощенная функциональная схема (без раскрытия структуры блоков) описанной выше ЭМС. Здесь принято: УМ – усилитель мощности, ОУ – объект управления (электродвигатель), ДОС – датчик обратной связи. Поскольку T_У>>T, то дискретностью регулятора можно пренебречь и получить структуру, изображенную на рис3. 13.

Рис.3. 13

Возникает вопрос, как найти передаточную функцию структуры, изображенной на рис 3. 13? Ведь её входной сигнал E(s) непрерывный, а другой - выходной Y(z,0)-  дискретный. В литературе такие структуры называют "непрерывно - дискретными" и предлагают специальный математический аппарат для их исследования [46, 48]. Мы предлагаем более простое решение.

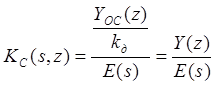.                                                                              (1. 13)

Приведем систему (рис. 3. 13) к более удобной расчетной структуре:

Рис. 4. 13

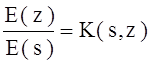                                                   (2. 13)

.                                                                                (3. 13)

Итак, появился дополнительный блок со специальной разно размерной передаточной функцией (РРПФ) K(s, z)¹⁾. Теперь структурную схему расчетной модели АДАС (АЦАС) можно представить в виде, изображенном на рис. 5. 13.

Рис.5. 13

Здесь появился "блок разно размерных преобразований" (БРП). Его передаточную функцию (РРПФ) можно раскрыть на основании выражения (3. 13) следующим образом:

,                            (4. 13)

где  и .

Таким образом, передаточная функция БПР разделилась на два сомножителя. Первый из них определяется свойствами сигнала управления , а второй - свойствами системы.

9. 5. 3. Характеристики и свойства блока разно размерных

преобразований

Рассмотрим оба сомножителя РРПФ БРП отдельно.

В первую очередь исследуем более сложный сомножитель Δ_сист (z,s), учитывая, что его передаточные функции числителя и знаменателя (уже не разно размерные) равны: Ф(z)=K(z,0)/[1+K(z,0)] и Ф(s)=K(s)/[1+K(s)].

,                                                                         (5. 13)