Процедуры модифицированного метода динамического синтеза для ИС и ЦАС. Расчётная математическая модель аналого-дискретно-аналоговой электромеханической системы, страница 2

  K(s)=D(s)×к_ук_д К_ЭК_О(s), K(z)=D(z)×{к_ук_дК_ЭК_О(s)}. Здесь к _у к _д К _Э(s)K₀(s) – произведение четырех ПФ: усилителя, датчика, экстраполятора и объекта.

______________________________________________________________________________

^*)Термины "разно размерная передаточная функция" (РРПФ), "блок разно размерных преобразований" (БРП) введены нами для удобства, без проверки лингвистической достоверности (С.К.)

Причем, без большой погрешности, мы упростили задачу, считая усилитель мощности и датчик безинерционными линейными звеньями.

Что делать с этим выражением (5. 13)? Анализируя величину его числителя  и знаменателя, рассмотрим состав ПФ K(s) и ДПФ K(z), а затем  перейдем к оценкам их модулей в частотой и псевдочастотной областях, соответственно.

Как мы помним, в низкочастотной области функции частоты и псевдочастоты близки и, практически, совпадают. На этом основании можно считать, что при низких частотах Δ_cис()≈1.

С другой стороны, в высокочастотной области К(jω) и К(jλ) вообще малы по абсолютной величине (поскольку мы рассматриваем устойчивую систему) – малы по сравнению с единицей, входящей первым слагаемым в числитель и знаменатель. Поэтому здесь также Δ_cис()≈1.

Вообще говоря, остается тонкий вопрос – а близко ли значение Δ_СИС(s,z) к единице в области границы частот, при λ=2/Т (ω=ω_K/4). При практических исследованиях можно просто вычислять значения модуля и фазы Δ_СИС(jω_K/4, 2/T) в этой точке и вводить поправку. Итак, со вторым множителем, входящим в состав K(s,z) мы, в целом, разобрались.

Теперь рассмотрим первый сомножитель. По сути, он является отношением аналогового и цифрового сигналов управления (мы, как обычно, рассматриваем единичные входные сигналы).

Примечание Р.Горковенко. Для соблюдения размерности нам следует перейти к безразмерному аргументу ‾t (тэ-надчеркнутое). Между прочим, откуда появился период квантования Т в формуле для G(s), – я, к своему стыду" не уследил?

Ответ С. Ковчина. Спасибо, Родион! Как всегда Вы поднимаете, "к стати", важный вопрос. Профану - то "до лампочки". У него всегда "машина" (программа) виновата в том, что модель того же двигателя с тем же ПИ регулятором, реализованным в аналоговом виде и программно "выдает "разные переходные процессы, различающиеся в тысячи и более раз!

Преобразования "Z" и w"оперируют с"безразмерным  временем" "n", а преобразование Лапласа "s" связано с реальным временем "t". Я пришел к пониманию этого, пожалуй, через пару месяцев "проб и ошибок" при оценке погрешностей преобразования информации в ДСАУ и САУ. Ведь в литературе этого нет! Точнее, "корифеи", которые пишут умные монографии считают, что это "и маленькому ёжику должно быть понятно". Мне же, порой кажется , что многие практически важные вопросы им "и в голову не приходят". Поэтому мы, инженеры  - прикладники, к пониманию неадекватного поведения наших аналоговых и цифровых моделей реальных систем вынуждены доходить сами.

Далее:

.

Поэтому можно записать, что

.                                                                   (6. 13)

Выражение (6. 13) позволяет точно вычислить функцию, учитывая, что есть однозначная связь: ω=2arctg(λT/2)/T.

Поэтому выходит для комплексно - значной функции,:

 – фазочастотная характеристика;                               (7¹. 13)

 амплитудо - частотная характеристика.  (7^!!. 13)

Таким образом, нам удалось получить ЛАХ исследуемого блока. Мало того, мы теперь можем даже построить асимптотическую ЛАХ:

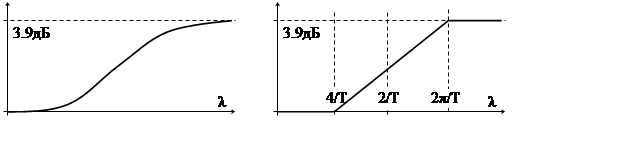Теперь мы можем позволить себе удовольствие иметь передаточную функцию нашего звена в виде

|K(λ)|=(1+Tλ/4)/(1+Tλ/2π).

Здесь прилагается полезная таблица 1: