Системы подчиненного управления (регулирования). Сравнительные характеристики параллельной и последовательной коррекций, страница 7

Если 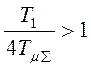 , то целесообразна настройка на симметричный оптимум. Главным образом по условию реализации регулятора. И чем больше это соотношение, тем целесообразнее симметричный оптимум.

Если 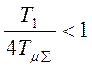, то лучше настраивать на модульный оптимум.

Данный вывод относится к отработке задающего воздействия. Аналогично и по условию отработки возмущения.

Сглаживание задающего сигнала

Настройка на симметричный оптимум при величине перерегулирования s = 43,4%  - нежелательна. Поэтому применяют меры по сглаживанию входного сигнала.

Передаточная функция оптимизированной замкнутой системы:

.

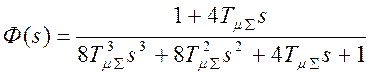Входной сигнал дифференцируется. Постоянная дифференцирования - - маленькая, поэтому имеем значительную по величине производную входного сигнала, являющуюся причиной столь значительного перерегулирования.

С целью уменьшения  производной и, как следствие, уменьшения перерегулирования, на входе замкнутой системы включается фильтр:

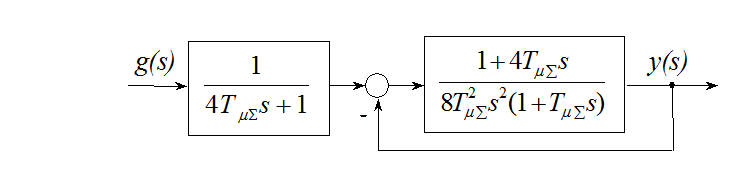
Тогда передаточная функция замкнутой системы с фильтром будет иметь вид:

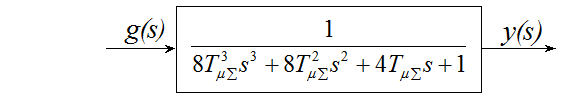
При этом изменяется переходная характеристика оптимизированной системы с фильтром:

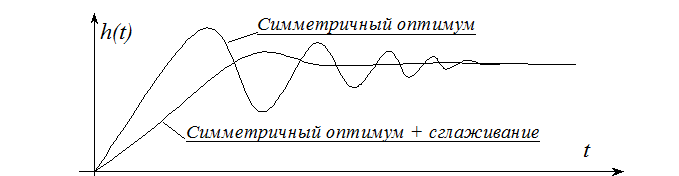
и ее основные параметры: ;  ;   .

Сглаживание при симметричной настройке в случае объекта

с большой инерционностью

На входе такой системы с целью уменьшения перерегулирования в случае симметричной настройки также устанавливается фильтр:

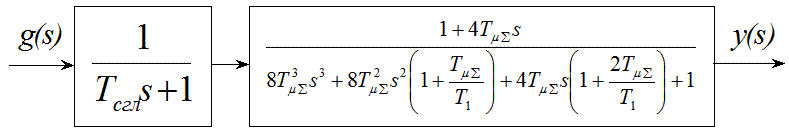
причем постоянная фильтра определяется:    .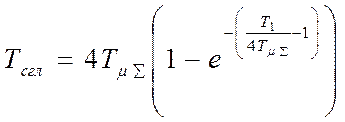

В этом случае, как и в предыдущем,   настроенная на симметричный оптимум система с фильтром обладает характеристиками:

;   ;    .

Эквивалентирование оптимизированного контура

В системах подчиненного управления настройка контуров выполняется последовательно от внутреннего к внешнему. Каждый из них настраивается на тот или иной оптимум. После настройки очередного контура его передаточная функция соответствует звену второго (модульный оптимум) или третьего (симметричный оптимум) порядка и входит составной частью в объект управления следующего по уровню контура. Сложный вид передаточной функции оптимизированного контура не всегда удобен для последующего использования. Ниже предлагается инженерный способ ее упрощения.

Пусть контур настроен на модульный оптимум. Переходная характеристика оптимизированного контура имеет вид:

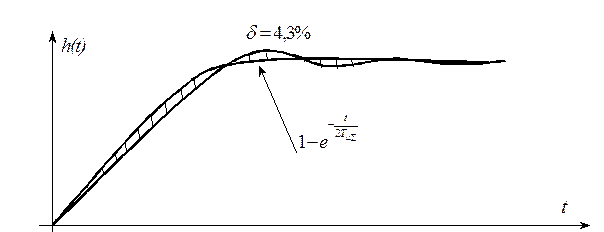
На том же графике приведена экспонента с постоянной  времени  .

Причем заштрихованные площади сверху и снизу от переходной характеристики равны. Таким образом можно примерно положить, что

.

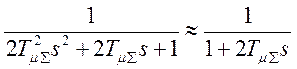Это равенство при последующем использовании будет более точным, если в объекте кроме  имеются еще малые постоянные времени. Тогда при настройке на модульный оптимум перерегулирование s = 4,3%.

Если кроме маленького колебательного звена в оптимизируемом объекте нет больше звеньев с малыми постоянными, то при последующей настройке на модульный оптимум перерегулирование  составит s = 8%. В этом случае звено, ранее настроенное на модульный оптимум, подлежит эквивалентированию апериодическим звеном, причем постоянная  может быть выбрана из следующих соображений:

если принять ,  то s = 8%, а если , то s = 4,3%.

При настройке на симметричный оптимум перерегулирование составляет s = 43,4%. Здесь подобрать эквивалентную экспоненту по площади или близкую по форме не удается. Да кроме того симметричный оптимум в чистом виде не применяется.

В том случае, когда на входе контура, настроенного на симметричный оптимум, установлен фильтр, величина перерегулирования в системе с фильтром s = 8,1%. Здесь также правомочна замена на апериодическое звено:

.

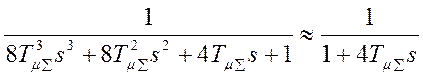При этом общее перерегулирование s = 8,1%.

В данном случае имеет место эквивалентная замена переходной характеристики экспонентой с постоянной времени .

Пусть объект, содержащий большую постоянную времени, настроен на симметричный оптимум. И последовательно с контуром также установлен фильтр.  Передаточная функция такой системы

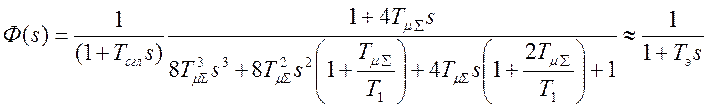
также упрощается, причем постоянная времени  эквивалентного апериодического звена будет равна 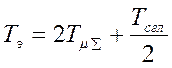 . Такая замена применяется всегда, когда постоянная фильтра удовлетворяет неравенству .

На практике для улучшения переходной характеристики оптимизированного контура с объектом, содержащем большую постоянную времени (смотри предыдущий случай), наряду с фильтрацией производится дифференцирование входного сигнала.

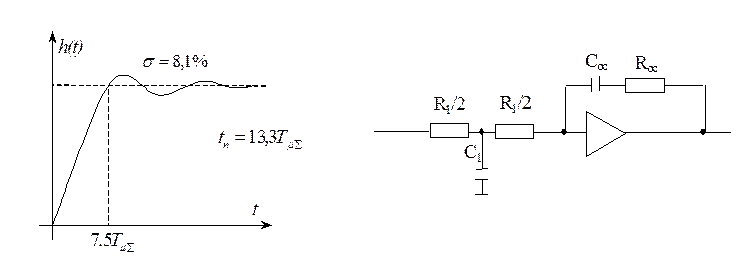
Параметры С₁ и R₁ подбираются опытным путем.