Информатика и выч. техника \ Вычислительные машины, системы и сети

Системы подчиненного управления (регулирования). Сравнительные характеристики параллельной и последовательной коррекций, страница 2

Сигналом управления (задания) gi  для i-го контура является выходной сигнал регулятора Wp,i+1(s) (i+1)-го контура. Таким образом (i+1)-й контур выступает по отношению к  i-му контуру как управляющий, а  i-й по отношению к (i+1)-му как подчиненный.  Это касается всех контуров, кроме 1-го (подчиненный) и n-го (управляющий).

На 1-й (самый внутренний) контур почти всегда возлагается задача обеспечения максимального быстродействия, поэтому его регулятор настраивают чаще всего так, чтобы "скомпенсировать" инерционности в объекте контура. Нескомпенсированными остаются только малые постоянные времени, которые скомпенсировать либо невозможно, либо нецелесообразно.

При этом нужно понимать следующее. В системах электропривода таким внутренним контуром является контур управления током (моментом) привода. Регулятор тока совершает преобразование потока энергии, в отличие от внешних регуляторов скорости и положения, преобразующих поток информации. Поэтому основным ограничением быстродействия в контуре управления током являются предельные энергетические возможности двигателя.

Постоянные времени помехозащитных фильтров можно скомпенсировать, но нецелесообразно, а эквивалентные постоянные внутреннего оптимизированного контура нельзя компенсировать, так как данная компенсация собьет настройку в этом контуре.

Все контуры в системах подчиненного управления оптимизируются (настраиваются) на определенный оптимум.

Задачи оптимизации

Под оптимизацией понимается получение наилучших (в каком-то смысле) показателей процесса с учетом ограничений, имеющих место в данной системе, объекте.

Идеальным является процесс, когда ошибка при отработке входного воздействия равна нулю:  x = 0.

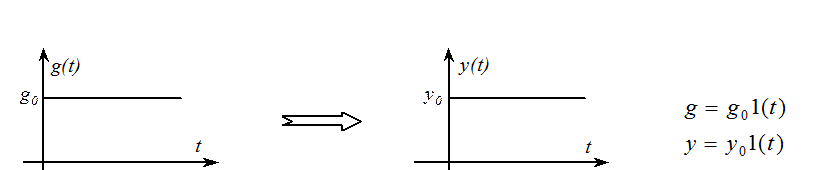
Если y= g, то ошибка равна нулю:  x = 0.

При наличии возмущения идеальной будет реакция системы, когда

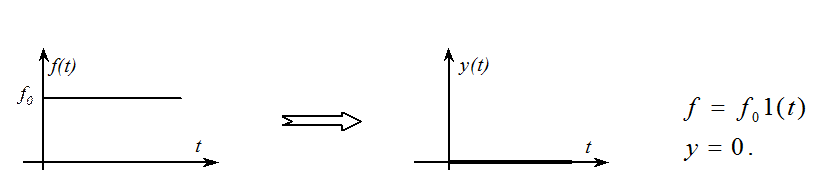
Следовательно, в идеальной системе    и        для  ω:  -¥ < w < ¥   или   0 < w < ¥.

Такая система нереальна, так как для мгновенной обработки входных сигналов моменты и усилия, создаваемые в системе должны быть бесконечными, что невозможно.

Сущность систем подчиненного управления заключается в том, что они представляют собой систему с компромиссной настройкой, когда к модулю амплитудно-частотной частотной характеристики  предъявляются следующие требования:

·  , то есть в области низких частот отработка сигналов идеальна,

·  отклонение  от единицы допускается в области высоких частот:

или 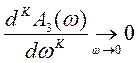   ,   К = 1, 2, 3, …

Кесслер предложил два типа оптимальных настроек, два оптимума:

1.  Технический (модульный),

2.  Симметричный.

Для модульного оптимума передаточная функция замкнутой системы должна иметь вид:

;          .

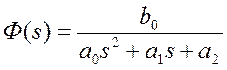Настройка контура на модульный оптимум заключается в приведение его к звену второго порядка с определенными параметрами.

Для симметричного оптимума передаточная функция замкнутой системы должна иметь вид:

;                

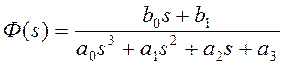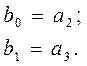
Настройка системы (контура) на тот или иной оптимум определяется особенностями объекта (зависит от его свойств, передаточной функции).

Таким образом, Кеслер предложил толькопо одной типовой настройке для систем второго и третьего порядков.

Общие сведения о регуляторах в системах подчиненного управления

Рассмотрим замкнутую систему, объектом управления которой является апериодическое звено.

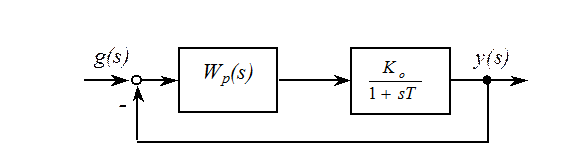
Реакция системы на входное воздействие, как будет показано, непосредственно зависит от структуры регулятора.

1.  П-регулятор (пропорциональный регулятор).

Его передаточная функция  .

Передаточная функция разомкнутой системы .

Передаточная функция ошибки в системе по заданию .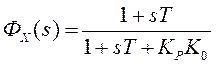

Статическая ошибка в системе при отработке постоянного входного воздействия определяется как 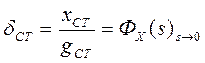 , или  , где - коэффициент усиления разомкнутой системы.

Вывод: П-регулятор, являясь безинерционным (что хорошо!), в то же время не устраняет статизм по заданию.

2.  И-регулятор (интегральный регулятор).

Соответствующие передаточные функции имеют вид:

,   ,   .

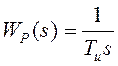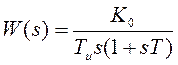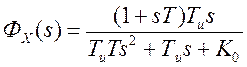Статическая ошибка в системе с интегральным регулятором равна:

.

Вывод: И-регулятор обеспечивает равную нулю ошибку по заданию, но является медленно действующим. Принципиально требуется время для интегрирования.

Скачать файл