3. ПИ-регулятор (пропорционально-интегральный регулятор).
Передаточная
функция регулятора 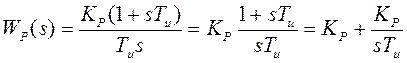 имеет
пропорциональную и интегральную составляющие: ПИ = П + И
имеет
пропорциональную и интегральную составляющие: ПИ = П + И
Передаточные
функции системы равны: 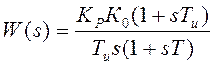 ,
,
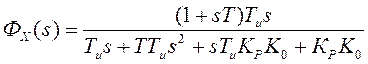 .
Ошибка в такой системе
.
Ошибка в такой системе ![]() .
.
С учетом правил преобразования структурных схем передаточная функция регулятора определяет структуру:
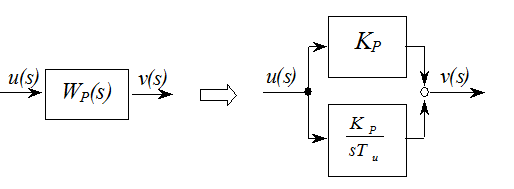
где отчетливо наблюдаются пропорциональная и интегральная части регулятора.
Вывод: ПИ-регулятор объединяет в себе достоинства П-регулятора (безинерционность) и И-регулятора (точность).
4. Д-регулятор (дифференциальный регулятор).
Передаточные функции системы с Д-регулятором:
![]() ,
, ![]() ,
,
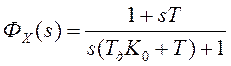 .
.
Ошибка в
системе с таким регулятором: ![]() .
.
Постоянная составляющая не поступает в систему (отсекается регулятором).
Вывод: Система с Д-регуляторм неработоспособна. Положительное качество - в упреждающем действии в динамике. Например, при гармоническом входном воздействии выходной сигнал опережает на 900 (относительно входного).
5. ПД-регулятор (пропорционально-дифференциальный регулятор).
![]() ,
, 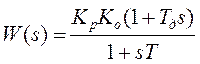 ,
,
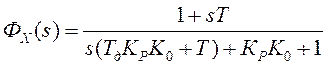 .
.
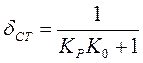 .
.
Вывод: ПД-регулятор работоспособен. В динамике обладает опережающим свойством. Недостаток: ПД-регулятор требует принятия мер для повышения помехоустойчивости, так как любое дифференцирование - плохой фильтр для помех.
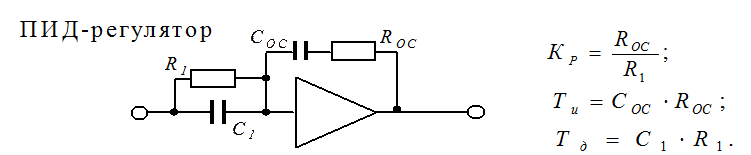
6. ПИД-регулятор (пропорционально-интегрально-дифференциальный регулятор)
В передаточной
функции ПИД-регулятора после соответствующего преобразования 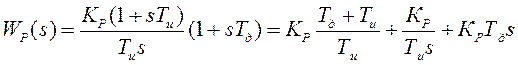 просматриваются все три его
составляющие: ПИД = П + И + Д .
просматриваются все три его
составляющие: ПИД = П + И + Д .
Передаточные функции системы: 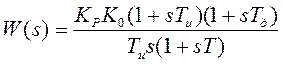 ,
,
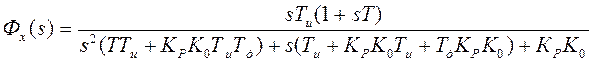 .
.
Ошибка в системе с
ПИД-регулятором: ![]() .
.
Вывод: ПИД-регулятор обеспечивает опережение по фазе в начале изменения сигнала, высокое быстродействие и нулевой статизм по заданию.
Принципиальные схемы регуляторов
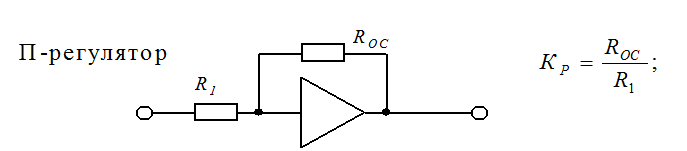
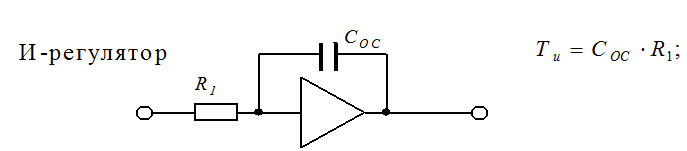
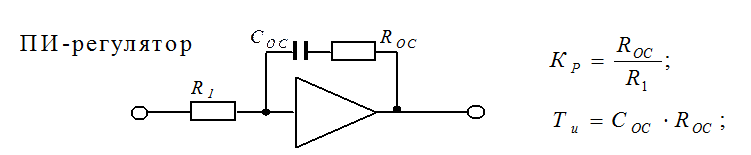
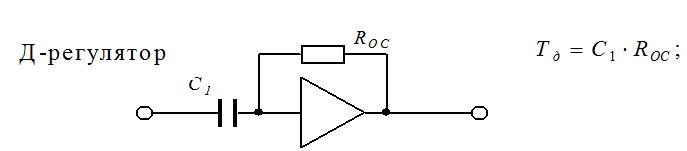
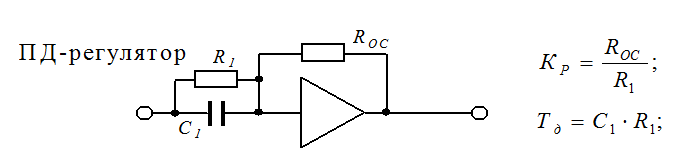
О сумме малых постоянных
Большинство объектов в системах автоматического управления описываются передаточными функциями вида
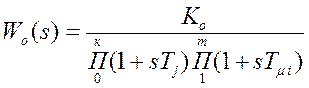 .
.
где Tj - большие постоянные времени,
Tm i - малые постоянные времени, причем Tm i << Tj .
Второй группе систем соответствуют объекты, в состав которых входят колебательные звенья:
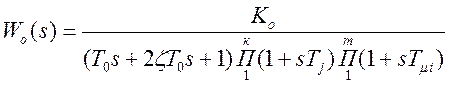 .
.
Такое разнообразие представляет определенные сложности и требует упрощения.
Итак, если в системе имеется несколько звеньев с малыми инерционностями, то с некоторым приближением их можно заменить одним эквивалентным звеном с суммарной постоянной времени. Покажем правомерность данной замены.
Рассмотрим два объекта с передаточными функциями:
1) ![]() и 2)
и 2) 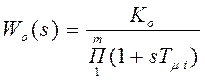 , причём
, причём 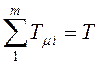 .
.
Последовательно с объектом включим И-регулятор (интегрирующее звено):
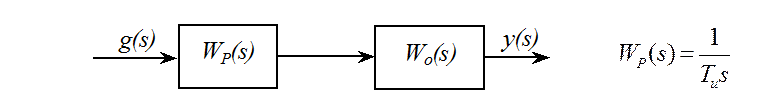
Реакция такой системы
на постоянное входное воздействие g(t)=g0=Const
в зависимости от объекта имеет некоторые различия. Чем больше количество малых
постоянных времени, составляющих 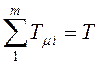 , тем ниже будет
расположена кривая h(t) до достижения времени
, тем ниже будет
расположена кривая h(t) до достижения времени 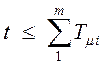 . В пределе при
. В пределе при ![]() переходная характеристика
соответствует реакции звена чистого запаздывания на g(t)=1(t).
переходная характеристика
соответствует реакции звена чистого запаздывания на g(t)=1(t).
На рисунке приведены переходные характеристики системы в зависимости от числа малых постоянных времени в объекте управления.

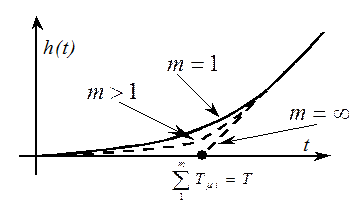
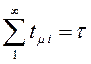 - постоянная звена чистого
запаздывания.
- постоянная звена чистого
запаздывания.
Анализируя переходные характеристики, можно заключить, что приближенная замена ряда апериодических звеньев с малыми постоянными времени на одно эквивалентное звено возможна. Необходимым условием такого эквивалентирования является наличие интегратора в последовательной цепи с объектом управления. Погрешность будет наблюдаться только в начальной части процесса. Тот же эффект наблюдается, если в объекте (последовательно с ним) имеется апериодическое звено с очень большой постоянной времени. Очень большая постоянная времени означает, что в начальный момент времени его реакция на ступенчатое воздействие похожа на реакцию интегрирующего звена:
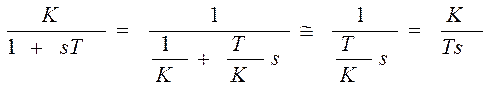 ,
когда К – велико, Т – велико.
,
когда К – велико, Т – велико.
Эквивалентная замена нескольких апериодических звеньев на одно может быть объяснена отбрасыванием членов со степенями s больше или равных 2 в следующем разложении:
![]()
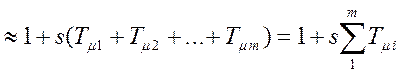 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.