В результате получаем 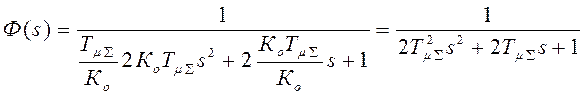 .
.
Сопоставим
параметры полученной передаточной функции системы, настроенной на модульный
оптимум, с параметрами колебательного звена 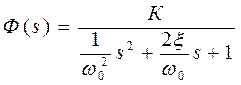 .
Сравнивая поэлементно, получаем:
.
Сравнивая поэлементно, получаем: 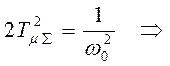
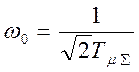 ,
, 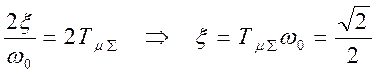 . Переходная характеристика:
. Переходная характеристика: 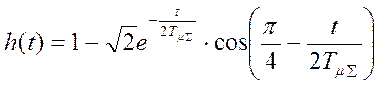 , σ = 4,3%,
, σ = 4,3%, ![]() ,
, ![]() .
.
2. Объект имеет одну большую и несколько малых постоянных времени:
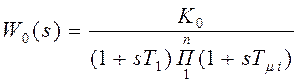 .
.
Выбираем регулятор ПИ-типа: 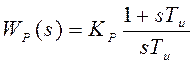 .
.
Тогда 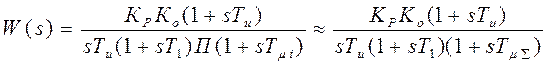 .
.
Если принять ![]() (компенсируем большую
постоянную времени), то
(компенсируем большую
постоянную времени), то
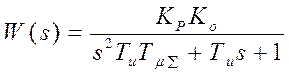 ,
,
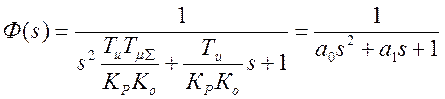 .
.
Потребуем выполнения условия ![]() :
: 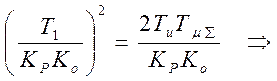 получим
коэффициент усиления регулятора:
получим
коэффициент усиления регулятора: 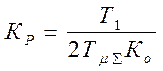 , а
передаточная функция замкнутой системы примет желаемый вид:
, а
передаточная функция замкнутой системы примет желаемый вид:
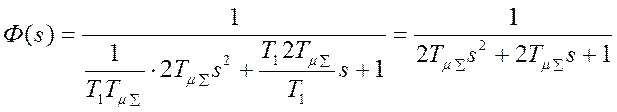 .
.
На модульный оптимум настроили!!!
3. Объект содержит две большие и несколько малых постоянных времени.
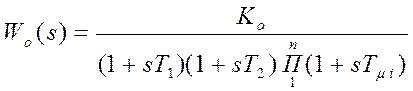 .
.
Выбираем регулятор ПИД-типа: 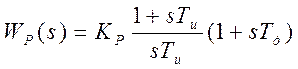 .
.
Полагаем: ![]() ,
, ![]() .
В результате по той же методике (выполнить
самостоятельно) получаем:
.
В результате по той же методике (выполнить
самостоятельно) получаем: 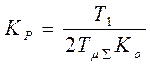 .
.
Деление постоянных времени на большие и малые
Имеется объект с передаточной
функцией 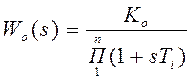 , гдеn = 4, Т1 = 0,4с, Т2 = 0,08с, Т3 = 0,015с, Т4 = 0,005с.
, гдеn = 4, Т1 = 0,4с, Т2 = 0,08с, Т3 = 0,015с, Т4 = 0,005с.
Рассмотрим следующие случаи:
1. Все постоянные
времени - малые. Тогда 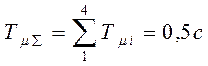 .
.
При настройке на
модульный оптимум выбирается И-регулятор с постоянной времени ![]() (численно). При этом параметры
переходной характеристики будут равны
(численно). При этом параметры
переходной характеристики будут равны ![]() ,
,
![]() (что плохо!!!) и σ = 4,3%.
(что плохо!!!) и σ = 4,3%.
2. Постоянная Т1 - большая, остальные -
малые. 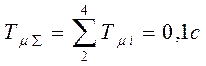 .
.
Регулятор в этом случае берется
ПИ-типа. Его параметры 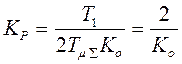 ,
, ![]() . В результате получается
модульный оптимум с характеристиками:
. В результате получается
модульный оптимум с характеристиками:
σ = 4,3%, ![]() ,
, ![]() (уже
лучше!!!).
(уже
лучше!!!).
3. Постоянные Т1 и
Т2 - большие, остальные
- малые. 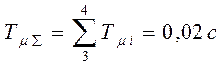 .
.
Регулятор ПИД -типа: ![]() ,
, ![]() ,
,
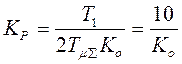 .
.
В итоге - модульный оптимум: ![]() ,
, ![]() (замечательно!!!),
σ = 4,3%,
(замечательно!!!),
σ = 4,3%,
4. Постоянные Т1,
Т2 и Т3 - большие, ![]() - малая.
- малая.
Регулятор ПИДД-типа: ![]() ,
, ![]() ,
,
![]() ,
, 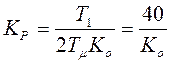 .
.
Модульный оптимум: σ = 4,3%, ![]() ,
, ![]() (отлично!!!).
(отлично!!!).
Но такой регулятор (и контур в целом) подвержен помехам. Его трудно настроить. А ввод фильтров уничтожит все достигнутое быстродействие.
Подведем
итоги. Передаточная функция замкнутого контура, настроенного на модульный
оптимум, имеет вид: 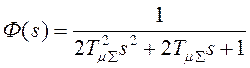 , соответствующая
передаточная функция разомкнутого контура:
, соответствующая
передаточная функция разомкнутого контура: 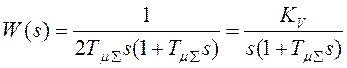 ,
где
,
где 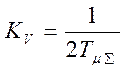 . Логарифмическая амплитудно-частотная
характеристика разомкнутого контура типа 1-2:
. Логарифмическая амплитудно-частотная
характеристика разомкнутого контура типа 1-2: ![]() ,
,
![]() ,
, ![]() , максимальный запас по фазе
, максимальный запас по фазе ![]() .
.
Формула Ямпольского Д. С.
До сих пор рассматривались объекты с малыми постоянными времени в прямом тракте. В общем случае малые инерционности могут буть и в обратной связи. Кроме того в системах могут встречаться и малые упреждения.
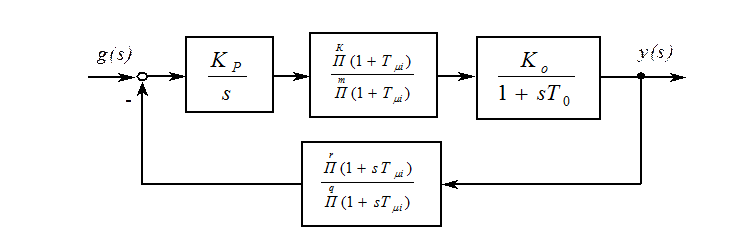
Как следует из
структурной схемы, предпринята попытка настроить систему на модульный оптимум
с помощью И-регулятора, у которого 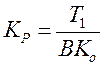 , где
постоянная В может быть определена
по формуле, называемой формулой Ямпольского:
, где
постоянная В может быть определена
по формуле, называемой формулой Ямпольского: 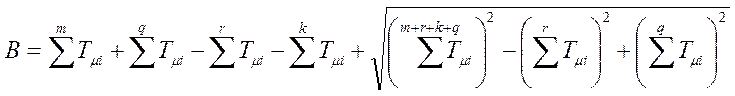 .
.
В результате передаточная функция
замкнутого контура примет желаемый вид 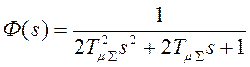 ,
а сумма малых постоянных
,
а сумма малых постоянных 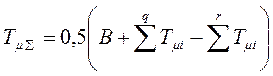 .
.
Настройка контура, если объект имеет очень большую инерционность
Пусть передаточная
функция объекта 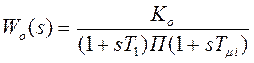 , причем
, причем ![]() . При настройке на модульный
оптимум ПИ-регулятор неприемлем, так как для его реализации необходимы очень
большие емкости.
. При настройке на модульный
оптимум ПИ-регулятор неприемлем, так как для его реализации необходимы очень
большие емкости.
Попробуем настроить с
регулятором П-типа: ![]() ,
, 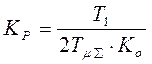 .
.
Тогда 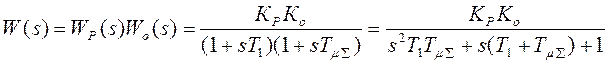 ,
,
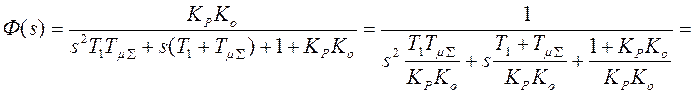
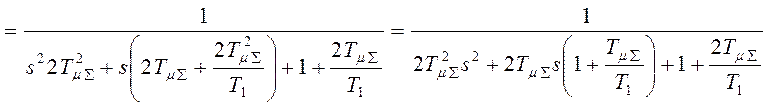 .
.
Получили настройку, похожую на модульный оптимум (по коэффициентам передаточной функции). Параметры переходной характеристики также близки к соответствующим значениям оптимальной системы. Но, к сожалению, имеет место статизм по заданию (статическая ошибка):
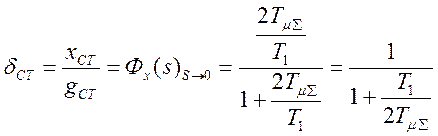 . При
. При ![]()
![]() .
.
Кроме ошибки по заданию в таким образом оптимизированной системе существует и составляющая ошибки, вызванная наличием возмущения,
величина которой определяется как:
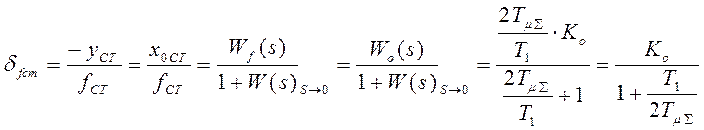 .
.
Из полученного
выражения следует, что статизм по возмущению непосредственно зависит от ![]() (статического коэффициента усиления
передаточной функции прямого тракта по возмущению
(статического коэффициента усиления
передаточной функции прямого тракта по возмущению ![]() ).
).
Симметричный оптимум
Настройка системы на модульный оптимум не всегда осуществима, например, если в объекте имеется интегрирующее звено. В отдельных случаях настройка на модульный оптимум бывает невыгодна, например, объект управления содержит апериодическое звено с большой постоянной времени. Тогда применяется альтернативная настройка на симметричный оптимум.
Отличительные черты (особенности) настройки на симметричный оптимум:
1. Симметричный оптимум, как и модульный, исходит из требования:
![]() и
и 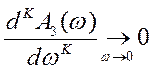 , К = 1, 2, 3, …
, К = 1, 2, 3, …
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.