Системы подчиненного управления (регулирования). Сравнительные характеристики параллельной и последовательной коррекций, страница 6

2.  Контур, настроенный на симметричный оптимум, имеет передаточную функцию третьего порядка:

   

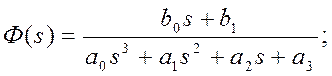
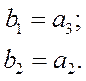
Соответствующая передаточная функция разомкнутой системы:

.

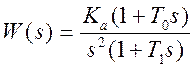Следовательно, система, настроенная на симметричный оптимум, обладает астатизмом 2 порядка (со всеми вытекающими отсюда свойствами).

Такой системе соответствует одна из трех ЛАХ с наклоном 2-1-2:

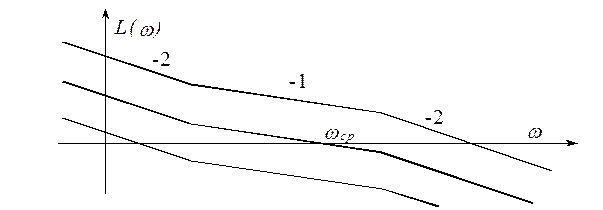
Как будет показано ниже, системе, настроенной на симметричный оптимум соответствует ЛАХ, частота среза которой находится на участке с наклоном -1.

3.  Переходная характеристика такой системы обладает бо^'льшим перерегулированием, чем при модульном оптимуме.

4.  Условия осуществимости симметричного оптимума иные, чем для модульного.

Обеспечим приближение модуля амплитудной частотной характеристики к 1 (единице) при :

Передаточная функция замкнутой системы .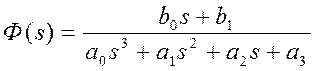

Модуль частотной характеристики (амплитудная характеристика системы)

.

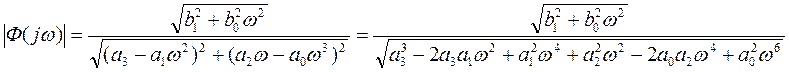Если потребовать   и   (условия приближения модуля частотной характеристики к единице),   то выражение для амплитудной характеристики системы упростится:      .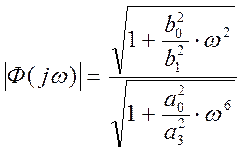

Кроме того, обычно выполняется:          но  

, тогда амплитудная (вещественная) характеристика замкнутой системы будет иметь вид:

Учитывая, что 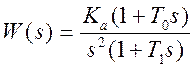, получим передаточную функцию замкнутой системы 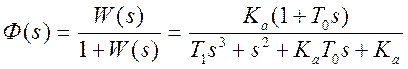. Используя условия приближения модуля частотной характеристики к единице:  и , получим, что 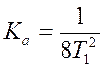  и  . При этом соответствующие передаточные функции системы, настроенной на симметричный оптимум, примут вид:

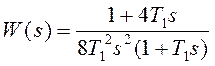  и  .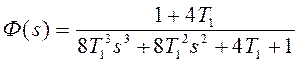

С учетом того, что при настройке системы на симметричный оптимум все большие постоянные времени объекта управления стараются скомпенсировать, а нескомпенсированными остаются только малые, то окончательно получаем:

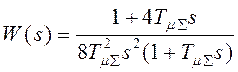  и  .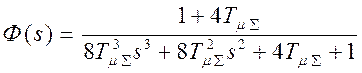

Полученные выражения являются эталонными, желаемыми, к которым требуется приводить передаточные функции системы в процессе настройки на симметричный оптимум путем соответствующего подбора регулятора.

Переходная характеристика оптимизированной системы имеет вид:

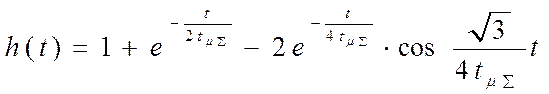
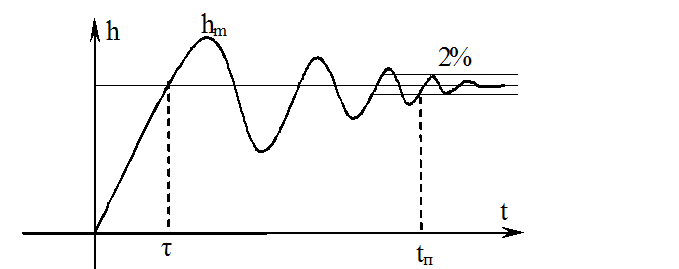
и обладает показателями:        ,   t = 3,1Т_mS ,   t_п = 16,5Т_mS. (аналогичные значения для модульного оптимума:   ,  t =  4,7Т_mS ,   t_п = 8,4Т_mS ).

Максимальный запас по фазе:

h.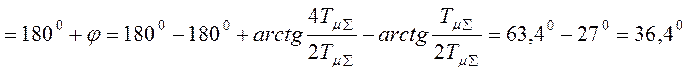

Тот же показатель для модульного оптимума составляет 63⁰. Здесь (при настройке на симметричный оптимум) - хуже.

ЛАХ разомкнутой системы изображена на рисунке:

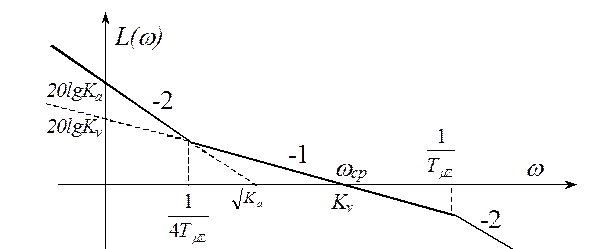
Основные параметры ЛАХ удовлетворяют соотношениям:

;     ;  ;   .

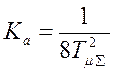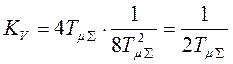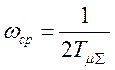Примеры настройки на симметричный оптимум

1.  Настройка на симметричный оптимум, когда объект содержит интегрирующее звено и малые постоянные времени.

Передаточная функция объекта:    .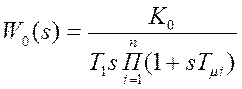

Выбираем регулятор ПИ-типа .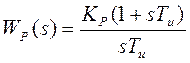

Тогда передаточная функция  разомкнутой системы

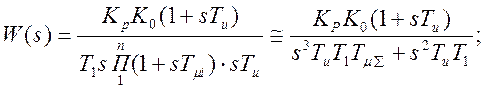
то же замкнутой -

.

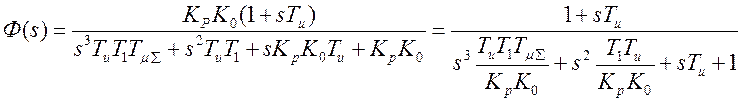Применим условия приведения модуля амплитудной характеристики к 1 (единице) и последовательно получим:

   ;

    .

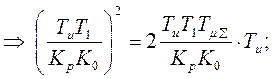
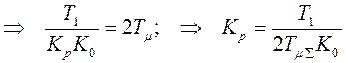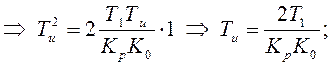
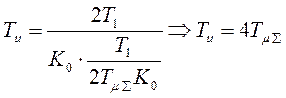После подстановки найденных К_р и Т_и в исходные выражения получим желаемые передаточные функции системы, настроенной на симметричный оптимум:

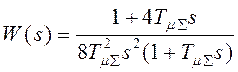  и  .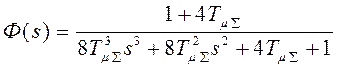

2.  Настройка на симметричный оптимум объекта, содержащего интегрирующее звено, одну большую и несколько малых постоянных времени.

Передаточная функция объекта:   .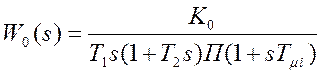

Выбираем регулятор ПИД-типа:    .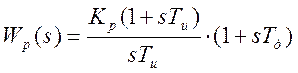

Если принять   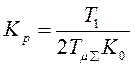       ,  то получим настройку на симметричный оптимум, при которой передаточные функции разомкнутой и замкнутой систем принимают желаемый вид.

3.  Настройка объекта, содержащего большую инерционность и несколько малых постоянных времени.

Передаточная функция объекта:  .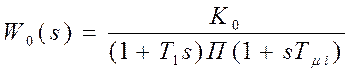

Пусть   . Контур может быть настроен на модульный оптимум!

А если попробовать настроить на симметричный?

Применим ПИ-регулятор: , ,     .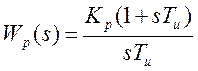

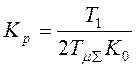Передаточные функции системы разомкнутой: 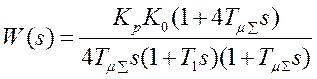   , замкнутой: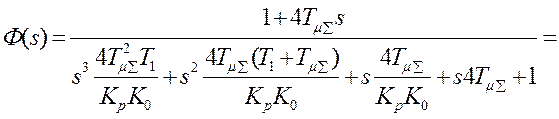   

.

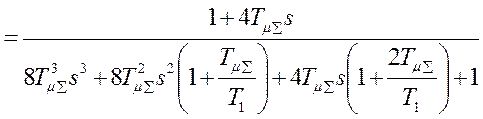Параметры настройки в зависимости от соотношения постоянных времени:

; ; .

если    - модульный оптимум,  - имеем симметричный оптимум.

Получили и не симметричный и не модульный оптимум!   Что-то среднее.

Пусть . Тогда после сокращения полиномов числителя и знаменателя:   

передаточная функция замкнутой системы примет вид:

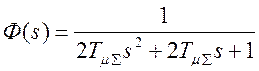, соответствующий чисто модульному оптимуму.

Вывод: Если имеется объект с большой постоянной времени, то контур может быть настроен как на симметричный, так и на модульный оптимум. Результат зависит от соотношения постоянных времени.