Информатика и выч. техника \ Вычислительные машины, системы и сети

Проблема устойчивости нелинейных систем и методы её решения. Постановка общей задачи исследования устойчивости движений динамических систем по Ляпунову, страница 9

Пример 2.  Пусть ЛЧ исследуемой НСАУ имеет такие же данные, как в Примере 1, но является астатической, то есть:

 Примем: .

Cоставим

Здесь вычислено:

. Итак, здесь одно неизвестное а3.. Составим для (ЛСАУ) Фл(р) определитель Гурвица и найдем предельное значение а3пр, которое "выводит" ЛСАУ на границу устойчивости. Это будет:

Δг=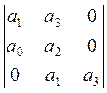. Отсюда имеем Получили: а3пр=0,6, rпр=0.06. Очевидно, такое значение неприемлемо, поскольку оно является предельно большим. Поэтому окончательно выберем r = 0.05.

Это были этапы предварительных расчетов. Только теперь и начинается исследование устойчивости модели НСАУ.

1. Найдем видоизмененную нелинейность . Она изображена в виде "зеленой" кривой  на рис. ниже. Её сектор теперь ограничен лучами κσ и rσ (а не лучем κσ и осью абсцисс, как в исходной системе). Теперь "угол" будет отсчитываться в новой декартовой системе координат, для которой осью абсцисс является луч rσ. Значение коэффициента "к" в новой системе координат будет: .

2. На плоскости АФЧХ разомкнутой системы проводим вертикаль . Она будет, естественно, расположена левее, чем исходная  .

Строим АФХ эквивалентной системы :

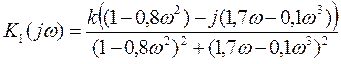. (Пример 1, при k= 10). Тогда при  ω = 0 кривая АФХ K1(jω)начинается в точке вещественной оси +10. Начальное значение эквивалентной АФХ астатической системы  будет  равно 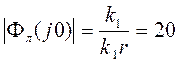. (Пример 2, при k1 = 10).

Итак, годограф  начинается в точке в два раза более удаленной, чем годограф статической системы. Поэтому и при частоте  годограф  пройдет левее вертикали . Следовательно, в модели ЛЧ коэффициент передачи можно уменьшить (например, взять k1=5,0), тогда r = 0,1. Характеристики K1(jω) и  начинаются в одной точке, но вертикаль  существенно левее .

Вывод. При заданных параметрах нелинейности и астатической ЛЧ данная нелинейная САУ неустойчива абсолютно в классе "0 – к".

Диссипативность и её использование для улучшения частотных условий абсолютной устойчивости

Для модели НСАУ запишем уравнение ЛЧ в виде:

 и  для нелинейности  .

Если матрица Н гурвицева и  нелинейность , при  k1<F(σ)<k2, отвечает неравенству

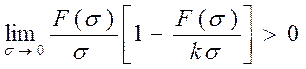, тогда модель НСАУ диссипативна.

При этом можно будет выбрать такое условие:

.

Критерий абсолютной устойчивости НСАУ В.М. Пòпова

Румынский ученый Василь Михай Пòпов в 1960 предложил свой вариант частотного критерия абсолютной устойчивости НСАУ с нелинейностью F(σ), принадлежащей к классу "0 - К". Локальная связь, в отличие от кругового  критерия устойчивости Якубовича, здесь характеризуется неравенством   ,                                             

Подобно теореме Лурье критерий Попова позволяет установить устойчивость нелинейной системы сразу для целого класса нелинейности, лежащих в секторе.

Пусть нелинейность F(σ) удовлетворяет частному условию:

, .

То есть нелинейность не выходит за рамки сектора в I и III квадрантах, при этом её конкретный вид не имеет значения, например, она может иметь  вид петли или быть сильно ломаной.

Понятно, что требования к виду нелинейности очень слабы, поэтому к данному классу нелинейностей относятся такие нелинейности, которые не поддаются обычным методам линеаризации вследствие недифференцируемости. Класс нелинейностей, умещающихся в секторе, очень широк, например, сюда относится большинство нелинейностей датчиков и приводов.

С другой стороны, сюда не попадает, например, обычное реле с гистерезисом.

Абсолютная устойчивость – это устойчивость для любой нелинейности внутри заданного сектора.

Устойчивость в целом(пространстве) – это устойчивость при любом начальном условии.

Устойчивость в целом является развитием вполне интуитивно понятной инженеру идеи: если график нелинейности F(σ) зажат границами сектора kσ, то коэффициент усиления нелинейности не "превышает k", и, если устойчива линейная система, в которой вместо F(σ) стоит  kσ, то должна быть устойчива и нелинейная система. Но для проверки устойчивости линейной системы можно использовать обычные критерии устойчивости, например, частотные.

Именно частотный подход используется в критерии Попова.

Скачать файл