Допустимое значение kл (k2>kл
>k1) определяется
решением задачи "минимальной устойчивости в данном классе". Для
этого, в расчетной модели НСАУ вместо нелинейности φ(σ) включаютлинейное
звено kл =const и записывают передаточную функцию расчетной замкнутой
линейной системы 
. По
критерию Гурвица вычисляют предельное значение коэффициента передачи кпр.
Эта величина kпр и
определит возможность охвата "окружности запрета". Фактически, это
означает выполнние условия "гурвицевости" матрицы Н. Термины
"минимальная устойчивось в данном классе" иусловие
"гурвицевости" матрицы Н однотипны. Они используются в разных
литературных источниках, но означают одно необходимость
выполнения второй гипотезы М. Айзермана для нелинейностей этого класса.
Очевидно одно, для НСАУ с "красной кривой"K3(jω)ЛЧ круговой критерий абсолютной устойчивости в изложенной формулировке не применим.
Случай 2. Рассмотрим применение этого критерия для оценки абсолютной
|
|
устойчивости НСАУ с нелинейностью, принадлежащей классу "0-k". Теперь есть только k2 ≠ 0, а k1 = 0, поэтому запретная область расширилась до окружности бесконечного радиуса. |
|
|
Условия
устойчивости НСАУ усложнились, поскольку K(jω) линейной части не могут
заходить за вертикальную прямую проходящую через точку с абсциссой |
Пример 1. Исследуем НСАУ с такими линейными частями:
и 
Примем: 
Найдем
АФХ линейных частей НСАУ. 
;
Вычислим частоту, при которой фаза равна
"π".
. Тогда
Итак, даже при том, что постоянная времени четвертого эвена в десять раз меньше, чем у третьего звена получили существенный заход K2(jω) в запретную зону (на 15%).
Случай 3. Рассмотрим применение кругового критерия для нелинейностей класса " k1-k2" при k1<0.
Если k1 отрицательная величина, то координата точки - 1/k1 приобретает положительное значение и "уходит" по вещественной оси вправо. Запретная зона для K(jω) ЛЧ существенно изменяется и будет распространяться на всю комплексную плоскость, кроме круга разрешенных для неё значений.
|
|
|
Для ЛЧ нелинейной системы разрешенная область для АФХ существенно снизилась. Например, для ЛЧ четвертого порядка при
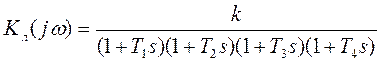имеем: 
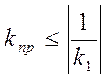при ω = 0, или
.
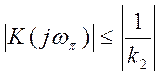Случай 4. ЛЧ системы в разомкнутом состоянии неустойчива, либо нейтральна (астатическая). Двое московских ученых В.А. Иванов и А. С. Ющенко предположили использовать круговой критерий абсолютной устойчивости в этом случае в измененном варианте.
Виктор Александрович Иванов и Аркадий Семенович Ющенко сотрудники московского государственного технического университета им. Н.Э. Баумана (МГТУ) - известные современные ученые в области теории управления.
Для этого структура НСАУ изменяется следующим образом. Параллельно нелинейности j(σ) вводится прямая отрицательная связь с коэффициентом r. Неустойчивая (или астатическая) структура K(s) охватывается отрицательной обратной связью с таким же коэффициентом r. Тогда получим новую структуру, которая будет эквивалентна исходной структуре при работе в автономном режиме.
Но "автономный режим" НСАУ (как и любой иной САУ) характеризует её свободное движение, то есть устойчивость. Поэтому такое предложение вполне приемлемо.
|
|
|
Докажем эквивалентность этих структур.
Приложение 1. Для замкнутой структуры (рисунок слева) составим
выражение операторной функции 
. Те
же операции выполним для правой структуры:
.
Тогда:
При 
имеем: 
или 
, или после простейших сокращений:
.
Следовательно, 
или
.
Откуда 
, но 
. Таким образом доказано: .
Итак, процедура оценки устойчивости НСАУ в этих случаях сводится к следующим операциям.
Составим ПФ замкнутой ЛЧ НСАУ (ЛСАУ)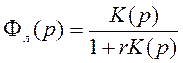 
. Определим
значение коэффициента r, решая задачу оценки устойчивости ЛСАУ с полученной
ПФ.
Далее сущность вопроса проще пояснять на конкретном примере.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
. На рисунке изображены АФХ ЛЧ
третьего и четвертого порядков с равными коэффицинтами передачи. Но
требования абсолютной устойчивости для НСАУ с ЛЧ четвертого порядка жестче.
Правда и область (сектор) возможных значений для 
больше.
