Чаще
решается обратная задача. Если задать матрицу ![]() (положительно
определенную симметрическую), например
(положительно
определенную симметрическую), например ![]() (единичную),
тогда производная функции Ляпунова будет отрицательной
(единичную),
тогда производная функции Ляпунова будет отрицательной ![]() . В этом случае если матрица H,
найденная из уравнения (14), является положительно определенной матрицей, то
система (11) – асимптотически устойчива в целом (матрица А имеет
собственные числа с отрицательными вещественными частями), иначе система будет неустойчива.
. В этом случае если матрица H,
найденная из уравнения (14), является положительно определенной матрицей, то
система (11) – асимптотически устойчива в целом (матрица А имеет
собственные числа с отрицательными вещественными частями), иначе система будет неустойчива.
Сформулирована и доказана следующая теорема:
Необходимое и достаточное условие асимптотической устойчивости в целом положения равновесия линейной автономной системы (11) заключается в том, что для произвольной симметрической положительно определенной матрицы G существует симметрическая положительно определенная матрица H, найденная из уравнения (14).
Следствие. Если начало координат линейной автономной системы (11) устойчиво, то существует единственная функция Ляпунова вида (12), где матрица H удовлетворяет уравнению (14), и G - произвольная положительно определнная матрица.
V-функция А.И. Лурье для нелинейных систем
Исключительно важное практическое значение имело предложение (1951г.) Анатолия Исааковича Лурье о V-функции для системы с единственной нелинейностью.
А. И. Лурье (1901г. – 1980г). В 1925г. закончил "физико-механический факультет Политехнического института. В 28 лет (1929 г) профессор. В 32 года доктор технических наук (1933г.). Чл. корр. АН СССР (1961г.). Организатор и первый заведующий кафедрой "Динамика и прочность машин" (теперь "Механика и процессы управления").
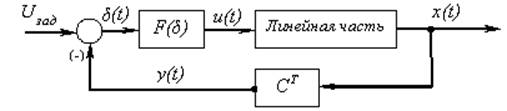
Пусть
имеется замкнутая САУ со статической сосредоточенной нелинейностью вида F(δ). Это может
быть любая комбинация линейных и нелинейных звеньев, частью охваченных
линейными или нелинейными обратными или прямыми связями. Лишь бы была известна
их обобщенная аналитическая характеристика F(δ). ЛЧ системы – статическая, то есть не имеет астатизма
любой степени и неминимально фазовых звеньев в знаменателе![]() .
.
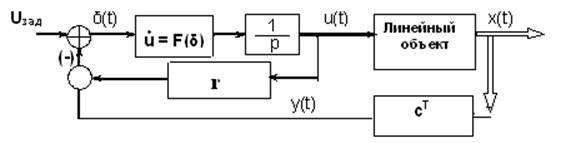
Система описывается следующими уравнениями:
Объект: 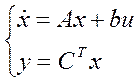 .
Нелинейность
.
Нелинейность ![]() :
: 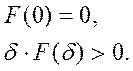
(Нелинейность находится в I и III квадрантах).
![]() , где r –
коэффициент местной OОС. Данная система является системой непрямого
регулирования (например, система управления летательными аппаратами,
где гидравлический привод перемещает рулевые органы, изменяя тем самым движение
летательного аппарата).
, где r –
коэффициент местной OОС. Данная система является системой непрямого
регулирования (например, система управления летательными аппаратами,
где гидравлический привод перемещает рулевые органы, изменяя тем самым движение
летательного аппарата).
Введем
замену переменных ![]() , обозначая
, обозначая ![]() . Тогда исходная система будет приведена
к системе прямого регулирования, описываемой уравнениями
(получены при условии
. Тогда исходная система будет приведена
к системе прямого регулирования, описываемой уравнениями
(получены при условии ![]() ):
):
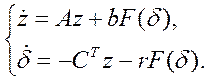 (15)
(15)
Как уже было сказано, А.И. Лурье предложил для рассматриваемой системы функцию Ляпунова вида (10):
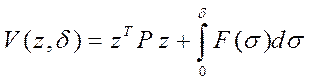 .
.
Функция Ляпунова является положительно определенной, если положительны оба слагаемых, ее составляющие.
Производная
V-функции: ![]() .
.
После
ряда подстановок и преобразований (с учетом замены ![]() и
и ![]() ) получаем:
) получаем: ![]() . (16)
. (16)
Матрица Q– произвольная симметрическая положительно определенная (тогда и матрица Р, получаемая в результате решения уравнения Ляпунова, также будет положительно определенной).
Выражение (16) может быть записано в виде:
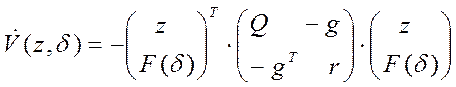 . (17)
. (17)
Для
отрицательности ![]() необходимо, чтобы
матрица
необходимо, чтобы
матрица 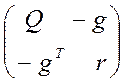 была положительно определенной, а
для этого достаточно, чтобы ее определитель был положительным, поскольку
матрица Q –
уже положительно определенная. Введем матрицу
была положительно определенной, а
для этого достаточно, чтобы ее определитель был положительным, поскольку
матрица Q –
уже положительно определенная. Введем матрицу  ,
определитель которой положителен, а 0 – нулевой вектор. Отсюда следует, что определитель
произведения этих матриц
,
определитель которой положителен, а 0 – нулевой вектор. Отсюда следует, что определитель
произведения этих матриц
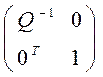 .
.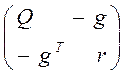 =
=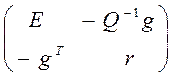
также
должен быть больше нуля: ![]() , или
, или
![]() . (18)
. (18)
При выполнении неравенства (18) введенная функция (10) действительно является функцией Ляпунова, а исходная система будет абсолютно устойчива.
Для системы прямого регулирования:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.