Информатика и выч. техника \ Вычислительные машины, системы и сети

Проблема устойчивости нелинейных систем и методы её решения. Постановка общей задачи исследования устойчивости движений динамических систем по Ляпунову, страница 4

·  Знакоопределенная V-функция. Это такая функция, которая во всем пространствеG[V(t)] имеет один знак, кроме начала координат, где она принимает нулевое значение.

·  Знакопостоянная V-функция – функция, принимающая во всем пространствеG[V(t)] либо значения одного знака, либо нулевые значения (включая начало координат).

Одновременно с функцией Ляпунова  рассматривается другая функция: W, 

На рисунке изображены V1 , V2 – знакоопределенные, а V3 - знаконеопределенная функция.

Значит, если функции V1 и V2 являются положительно определенными, то для устойчивости соответствующего  процесса достаточно, чтобы функции W1 и W2 были отрицательными или тождественно равнялись нулю.

Однако для функции V2, функция W2  принимает и положительные и отрицательные и нулевые значения. Поэтому достаточному условию устойчивости "в большом" удовлетворяют лишь динамические процессы НСАУ с V-функциями Ляпунова подобными V1.  НСАУ второй структуры (V2 , W2) станет устойчива "в малом".  Функция V3 – знаконеопределенная. Следовательно, динамические процессы в третьей НСАУ неустойчивы "в большом".

Здесь V и W – "принадлежат", соответствуют процессу, системе.

Для прямого метода устойчивости А. М. Ляпуновым сформулировано две теоремы.

Теорема 1.  Достаточным условием устойчивости динамических процессов "в большом" будет знакоопределенность V-функции и знакопостоянство W функции противоположного знака.

Теорема 2. Если при знакоопределенности V-функции, W-функция также будет знакоопределенна (но другого знака), то динамический процесс в НСАУ будет устойчив асимптотически "в большом" (то есть заканчиваться покоем системы).

Сложность применения прямого метода Ляпунова для оценки устойчивости динамических процессов "в большом" заключается в нахождении V-функций для конкретных моделей НСАУ. К настоящему времени функции Ляпунова построены практически для всех наиболее важных классов нелинейных систем, встречающихся на практике.

Например, для системы с единственной нелинейностью φ(σ) функцию Ляпунова А.И. Лурье (совместно с В.И. Постниковым) предложил принять в виде:

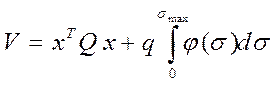,                                                                                                                (10)

где Q - матрица размерности n´n –  положительно определенная (поэтому слагаемое  будет знакоположительной величиной),  а q – некоторое положительное число. Если нелинейность φ(σ) принадлежит классу "0 - К", то есть , то  и сама функция Ляпунова будет знакоопределенной.

Кроме того, если функцию Ляпунова можно построить, то через нее удается выразить динамические показатели качества системы: перерегулирование и время переходного процесса.

Исследование устойчивости линейных систем с помощью  прямого метода Ляпунова

Рассмотрим линейную стационарную систему .                                                                                                              (11)

Пусть положение равновесия системы (11) находится в точке . Будем искать функцию Ляпунова в виде                                                                                                                 (12)

с положительно определенной симметрической матрицей Н.

Производная этой функции в силу уравнения (11) имеет вид:

.                                                                                                              (13)

Получили квадратичную форму. Поэтому чтобы производная по времени от функции Ляпунова (12) была отрицательно определенной, квадратичная форма (13) должна быть отрицательной, а матрица   - отрицательно определенной. Обозначим 

.                                                                                                              (14)

Кроме того , то есть матрица G – симметрическая. Уравнение (14) относительно матрицы H называется уравнением Ляпунова.

Скачать файл