Проблема устойчивости нелинейных систем и методы её решения. Постановка общей задачи исследования устойчивости движений динамических систем по Ляпунову, страница 10

Критерий Попова дает критерий абсолютной устойчивости в целом и формулировка его подобна критерию устойчивости Найквиста.

Пусть линейная часть задана операторной функцией W(p), нелинейная часть находится в секторе k. Пусть можно найти такое число q, что выполняется следующее частотное неравенство:

.

Тогда система является абсолютно устойчивой в целом и, кроме того,    при .

Данное частотное неравенство имеет геометрическую интерпретацию, подобную критерию Найквиста. Раскроем это выражение:

.

То есть 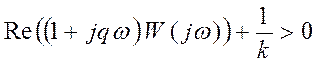   фактически означает:  

.

Если ввести модифицированный годограф:

, то частотное неравенство для модифицированного годографа принимает вид:

.

В самом деле, это условие просто означает, что модифицированный  годограф должен находиться правее прямой, проходящей через точку (-1/k ; j0) с угловым коэффициентом qна комплексной плоскости с координатами .   С другой стороны, можно выбрать в качестве "нелинейности" границу сектора:  F(σ) = kσ.  Такая нелинейность входит в рассматриваемый класс, но при её наличии система линейна, и для неё, как для линейной, можно использовать необходимое и достаточное условие Найквиста. Это в данном случае означает, что обычная АФЧХ линейной части не должна "охватывать" точку (-1/k ; j0) (так как W(jω)k не должна "охватывать" точку (-1; j0).)

·  Следовательно, необходимым условием, дополнительным к критерию Попова, будет условие, чтобы обычный (немодифицированный) годограф линейной части не пересекал вещественную ось левее точки -1/к.

·  Отметим, что условие Попова - лишь достаточное, поэтому критерий позволяет отсеять неустойчивые системы.

На самом деле, возможны три характерных случая. Рассмотрим пример, в котором  нелинейность заключена в секторе с k = 1. Тогда для устойчивости прямая в критерии Попова должна проходить через точку (-1; j0) с некоторым наклоном q, и график модифицированного годографа должен быть целиком правее.

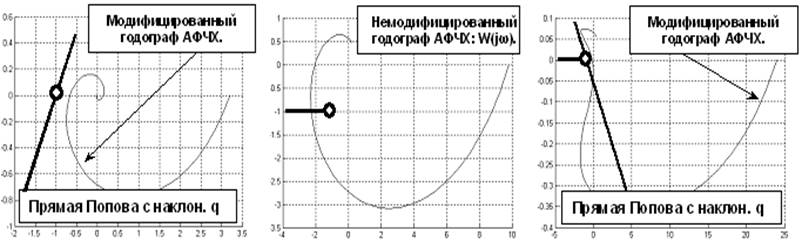
На левом рисунке система устойчива, так как имеется возможность провести через точку (-1; j0) прямую так, что годограф целиком оказывается справа.  На среднем - годограф немодифицированной АФЧХ линейной части пересекает вещественную ось левее точки -1/к = -1  (-1; j0). Система – неустойчива.

На правом рисунке невозможно провести прямую через точку (-1; j0) так, чтобы годограф оказался целиком правее, но это не значит, что система неустойчива. В этом случае требуется дополнительное исследование системы другими методами, отличными от критерия Попова.

Правило применения критерия Попова

·  На комплексной плоскости строится модифицированный годограф.

·  Отмечается точка -1/k,  определяемая сектором нелинейности.

·  Пытаются провести через эту точку какую-нибудь прямую с наклоном qтак, чтобы годограф оказался правее. Система будет абсолютно устойчивой, если это возможно.

·  Учитывают, что критерий Попова – только достаточное условие.

Итак, необходимые и достаточные условия абсолютной устойчивости не совпадают. Чтобы сблизить необходимое и достаточное условия приходится накладывать более жесткие ограничения на нелинейность. Двигаясь по этому пути, можно получить много обобщений критерия Попова, в частности, при дополнительных ограничениях на нелинейность можно использовать не модифицированный, а обычный годограф АФЧХ. Если нелинейность удовлетворяет такому дополнительному условию:  , то есть, скорость возрастания нелинейности ограничена в каждой точке величиной k, то в этом случае вместо модифицированного годографа можно использовать обычный (критерий Чо-Нареандры).

Подобных обобщений проделано великое множество. Один из них так называемый круговой критерий, который позволяет исследовать устойчивость при нелинейностях в более сложном секторе и, кроме того, нестационарных.

Имеются также обобщения критерия Попова на случаи других свойств линейной части, например, при наличии интеграторов.

Применение критерия Пòпова для определения предельного значения коэффициента передачи  линейной части системы

Для основного случая применения критерия Пòпова нелинейность φ(σ) должна быть расположена в секторе "0-К". Кроме того, известно, что есть некоторый предельный коэффициент передачи кпр ЛЧ. По второй гипотезе Айзермана значение кпр определяет границу устойчивости замкнутой системы с нелинейностью φ(σ), линеаризированной секущей.