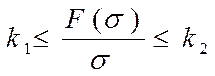Информатика и выч. техника \ Вычислительные машины, системы и сети

Проблема устойчивости нелинейных систем и методы её решения. Постановка общей задачи исследования устойчивости движений динамических систем по Ляпунову, страница 7

 для    и                                                                                                                 (20)

Таким образом, F(ζ ,σ) есть квадратичная форма вещественных переменных ζ и σ.

2. Характеристика  удовлетворяет интегральной связи с квадратичной формой  (19), если существуют  и  число Г > 0, такие, что выполняется неравенство

.                                                                                                                                    (21)                                                                     

Следовательно, требуется, чтобы интеграл при возрастании времени не стремился к отрицательной бесконечности. При выполнении локальной связи  (19) выполняется и интегральная связь (21) с той же формой F(ζ ,σ). Обратное утверждение не имеет силы. Можно найти функции, удовлетворяющие условию интегральной связи, но не имеющие локальной связи с формой F(ζ ,σ).

На основе выражений локальной и интегральной связей, уравнений для ЛЧ и НЧ системы в её свободном движении:

 и их преобразований, В. А. Якубович получил формулу  достаточного условия  частотного критерия

абсолютной устойчивости:

,                                                                                                              (22)

Здесь  и  - комплексно - сопряженные АФХ ЛЧ системы.

Если характеристика нелинейности имеет локальную связь с квадратичной формой (19), то модель НСАУ обладает абсолютной экспоненциальной устойчивостью в данном классе. Это значит, что можно найти положительные величины С и α, при которых свободное движение исследуемой системы будет асимптотически затухающим (по абсолютной величине):

.                                                                                                                    (23)                                                                     

На основании достаточного условия  частотного критерия абсолютной устойчивости (22) найдем удобное для  практического применения толкование кругового критерия абсолютной устойчивости.

Из неравенства  (22)  после преобразований  получим:    

.                                                                                                                        (24)                                    

Это выражение позволяет составить уравнение границы запретной зоны для АФХ линейной части системы:

.                                                                                                              (25)

Для участка границы (25), расположенного на вещественной оси, приняв P= x  и  Q= 0, получим:  .                                                                                                                (26)

Случай 1.  Решая уравнение (25) с учетом (26),  получим окружность:

радиусом , с координатой центра ,  проходящую через точки  и .

Итак, имеем запретную область, куда не должна заходить амплитудо-фазная характеристика  ЛЧ системы.

Следовательно, совместное изображение "запретной" окружности и частотной характеристики ЛЧ должны выглядеть следующим образом:

Круговой критерий абсолютной устойчивости НСАУ для случая 1 формулируется следующим образом.

Достаточным условием абсолютной устойчивости модели НСАУ является необходимость устойчивости ЛЧ и отсутствие захода её АФХ K(jω) в запретную область, ограниченную окружностью с координатами на вещественной оси  и . Если при этом соблюдается условие "локальной связи" (19), то устойчивость будет асимптотической.

Нелинейная система с АФХ линейной частиK1(jω) ("черная" кривая) будет устойчива при коэффициенте передачи ЛЧ . Но можно ли выбрать иную ЛЧ ("синяя" кривая) при , чтобы K2(jω) охватывала "окружность запрета"?

Скачать файл