Проблема устойчивости нелинейных систем и методы её решения. Постановка общей задачи исследования устойчивости движений динамических систем по Ляпунову, страница 2

1. Пусть движения системы п-го порядка описывается п дифференциальными уравнениями первого порядка, записанными в форме Коши:

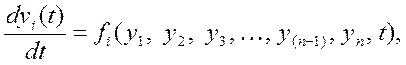   i=1, 2, 3,…                                                                                                                  (1)                                               

где y_i (t) - вещественная переменная (координата), характеризующая поведение НСАУ при известной характеристике нелинейности F(x) или F(x, px), f_i  - известная функция координат и времени.

Исходное состояние модели системы при t=t₀определяется начальными условиями .         (2)

3. Каждая совокупность начальных условий соответствует существованию единственного свободного решения системы  (1) при  t>t₀  в виде

,     i=1, 2, 3,…                      (3)                                                                                              

в некотором пространстве G[y_i(t)] возможных реализаций этих координат.

4. Свободные движения могут быть установившимися и неустановившимися, но все они являются возмущенными различными начальными условиями.

5. Произвольно назовем одно из таких движений невозмущенным и обозначим:

,    i=1, 2, 3,…                                                                                                          (4)                                                                                                                                                    

6. Изменим запись начальных условий, представив их в таком виде:

,  ,  ,  .                                                                                                                           (5)

Движения системы (1), определенные по формуле (3) с начальными условиями  (5), назовем возмущенными.

7. Введем новые переменные ,  i=1, 2, 3,…,                                                                                                         (6)

которые называют  вариациями - отклонениями.

Тогда условие устойчивости невозмущенного движения формулируется следующим образом.

Невозмущенное движение устойчиво по отношению к переменным x_i(t), i=1, 2, 3,…, если при всякой, сколь угодно малой положительной величине ε, можно выбрать другую величину δ так, чтобы при всех возмущениях (вариациях x_i(t), i=1, 2, 3,…) соблюдались следующие условия:

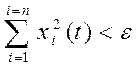, а при     .                                                                                                                (7)

В противном случае невозмущенное движение неустойчиво.

Очевидно, при 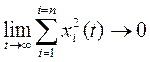 соответствует асимптотической устойчивости динамического процесса.

В условиях (7) ряд авторов вместо сумм квадратов записывают любые абсолютные значения отклонений, что не меняет сути метода. Если принять , то условие (7) означает, что только для устойчивых движений существует определенная область их притяжений  в область , охватывающая начало координат.

Пример. Замкнутая по скорости нелинейная электромеханическая система (ЭМС) имеет ПИ регулятор, нелинейный усилитель мощности, двигатель постоянного тока и тахогенератор - датчик обратной связи. Переменные модели ЭМС (y_i): угловая скорость вращения вала двигателя ω, преобразованная в сигнал напряжения задания U_з тахогенератором (y₄), напряжение на выходе усилителя мощности U_y(y₃), ток в якоре (роторе) двигателя I(y₂), магнитный поток машины Ф(y₁) и электромагнитный момент двигателя M(y₅).

Уравнение (1) в физической форме будет иметь такой вид:

.

Примечание. Пожалуй, единственное, что мы здесь не поясняем -  не даем описания конкретного решения этого уравнения.

То же уравнение НСАУ в переменных состояния  вида (1) будет:

.

Уравнения (2) будут (при различных начальных условиях) такими:

;

;

…………………………………..;

, где ,   ,   отдельные наборы (совокупности) начальных условий.

Все "к" решений дают возмущенные движения. Выберем в качестве невозмущенного движения y₄₂(t)= y_i^*(t). Тогда начальные условия возмущенного движения, выбранные в  физическом смысле постоянные величины: Ф₂(y₁₂), I₂(y₂₂), U_y2(y₃₂) ω₂(y₄₂), M₂(y₅₂) и будут представлять собою. .

На понятиях вышеуказанного примера поясним, что же такое "пространство G[y_i(t)] возможных реализаций переменных"?