Возможности среды Matlab для построения нейронных сетей, использование предоставленными возможностями

Санкт-Петербургский Государственный Политехнический Университет

Факультет Технической Кибернетики

Кафедра Компьютерных Систем и Программных Технологий

ОТЧЕТ

по практическому заданию №1

по предмету «Нейроинформатика»

Работу выполнил студент группы 3081\2 Гранько Никита

Преподаватель ____________

Санкт-Петербург

2010

1.  Цель работы

Узнать возможности среды Matlab для построения нейронных сетей, научиться пользоваться предоставленными возможностями

2.  Выполнение работы

2.1. Нейроны

2.1.1.  Simple neuron and transfer functions

При помощи этой функции, изменяя значения порогового коэффициента b и синоптического коэффициента w, а также выбирая вид функции активации f, мы можем наблюдать изменения на графике.

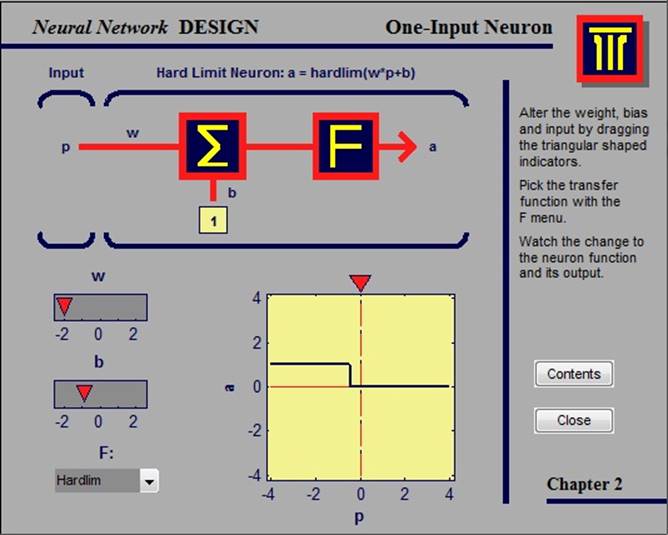
Возможные типы функции активации:

hardlim – пороговая функция

hardlims – пороговая функция с насыщением

purelin – линейная функция

satlin – линейная функция с насыщением

satlins – линейная симметричная функция

logsig – сигмоидальная функция

tansig – сигмоидальная симметричная функция (гиперболический тангенс)

2.1.2.  Neuron with vector input

В данном примере мы имеем дело с нейроном с двумя входными параметрами (two-input neuron), в котором, изменяя входные параметры p₁ и p₂ , значения порогового коэффициента b и синоптических коэффициентов w₁ и w₂ , а также выбирая тип функции активации, мы способны контролировать значения выходного параметра a, а также промежуточного параметра n

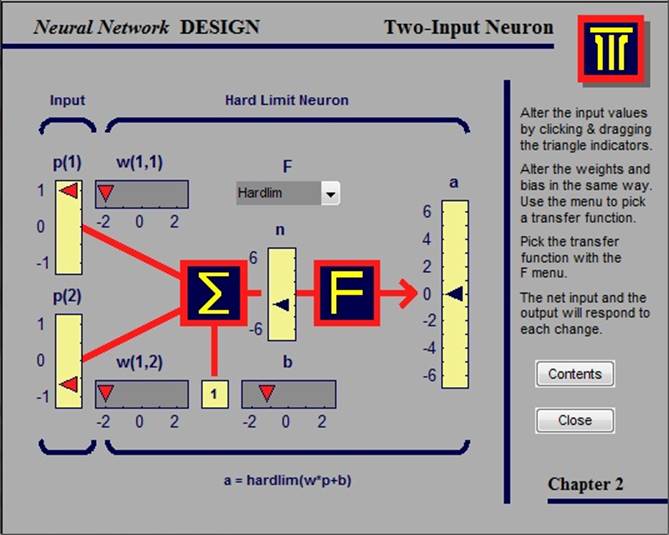
Возможные типы функции активации совпадают с таковыми из предыдущего примера.

2.2. Персептроны

2.2.1.  Decision boundaries

В данном примере рассматривается классификация входных векторов. Прямая, перпендикулярная матрице коэффициентов W разделяет область решения на две части. Входные векторы, располагающиеся выше данной прямой (на рисунке закрашены черным), соответствуют выходному значению, равному 1; векторы же, расположенные ниже прямой (закрашены белым), соответствуют выходному значению, равному 0. Сама прямая может быть свободно перемещена по области для достижения наилучшего  способа классификации, при этом изменяется пороговый коэффициент b. Если контур ни одного из кружков в данном примере не будет красным, значит, все сделано верно.

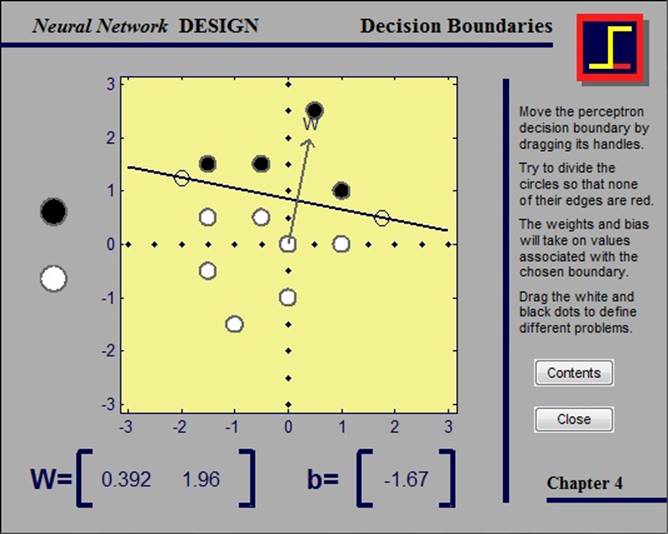
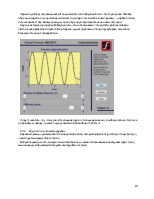
2.2.2.  Perceptron learning rule

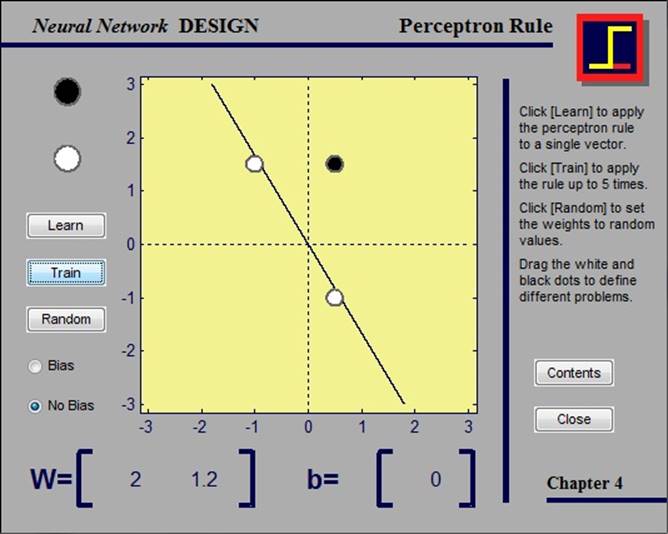
В данном примере рассматривается правило обучения персептрона. В нем пользователю дана возможность лично выбирать количество и расположение входных векторов и применять к данной комбинации правило обучения. Если решение для данной комбинации существует, то оно будет найдено за конечное число итераций.

Если ответ для данной комбинации найден не верно, то нужно изменить веса одновременно активных нейронов соответственно ситуации.

2.2.3.  Classification with a 2-input perceptron

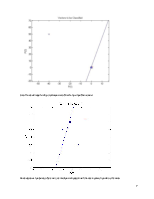
Данный пример иллюстрирует правило обучения персептрона с использованием среды Matlab. В нем рассматривается создание персептрона, определение весов входных векторов, разделение входной области на две части, соответствующие выходным значениям 0 и 1, а также определение категории нового входного вектора.

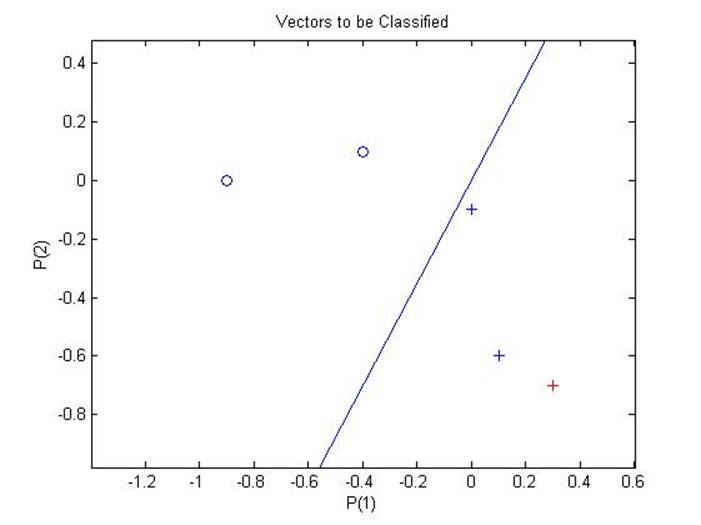
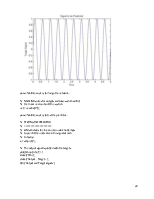
2.2.4.  Outlier input vectors

В данном примере рассматривается ситуация, в которой из-за входного вектора гораздо большей, нежели у остальных, длины, обучение персептрона будет занимать продолжительное время. Связано это с тем, что правило обучения персептрона в случае ошибки предусматривает вычитание или прибавление входных векторов к коэффициентам и порогам. С учетом отстоящего входного вектора эти операции будут длиться гораздо дольше, нежели в простейшем случае.

Вот так выглядит входная область после окончания обучения:

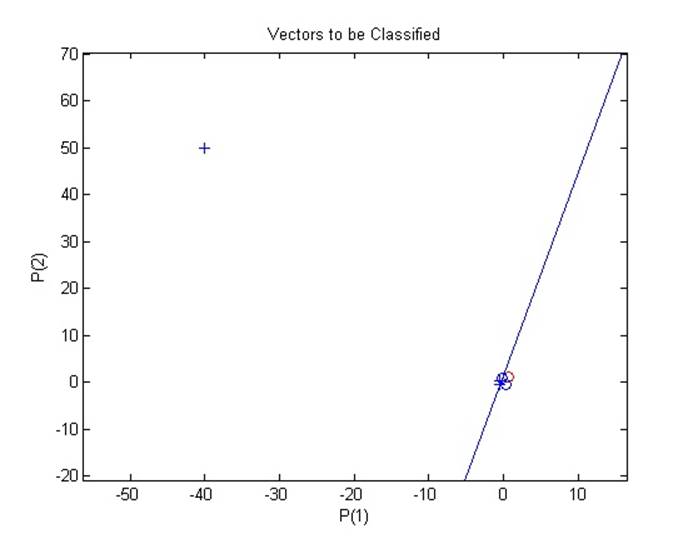
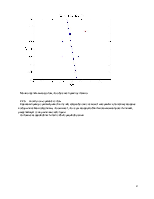
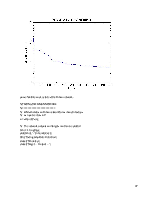
А вот так выглядит интересующая нас область при приближении:

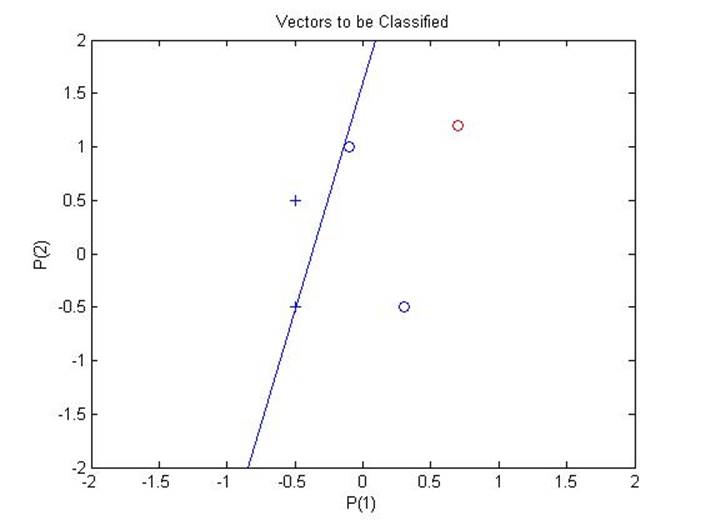
Как видно из графика, обучение, несмотря на продолжительное время, прошло успешно.

2.2.5.  Normalized perceptron rule

В данном примере мы имеем дело с ситуацией, схожей с предыдущей: один из векторов имеет гораздо большую длину, нежели остальные. Но в данной ситуации мы воспользуемся функцией learnpn, которая позволяет значительно сократить время на обучение персептрона, не уступая при этом в точности.

Вид входной области после окончания обучения:

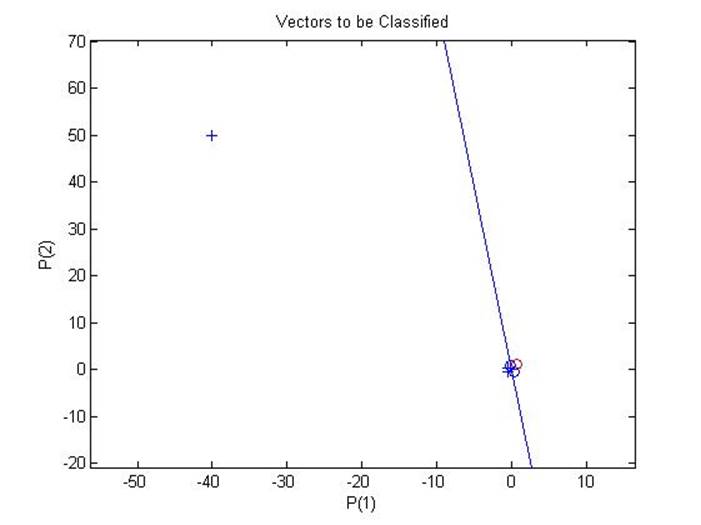
Приближая к интересующей нас области, получаем:

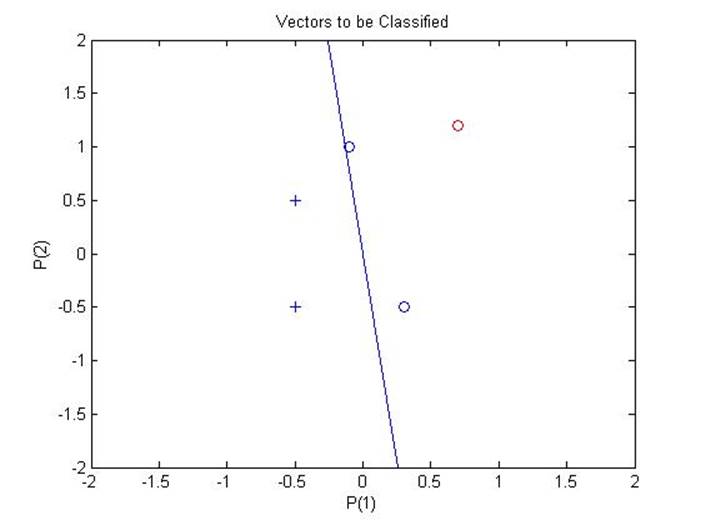
Можно сделать вывод о том, что обучение прошло успешно.

2.2.6.  Linearly non-separable vectors

В данном примере рассматривается случай, когда обучение не может завершиться, поскольку входные векторы линейно неотделимы, что означает, что через входную область невозможно провести линию, разделяющую ее на различные категории.

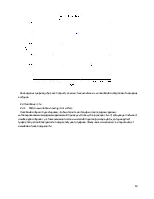
Состояние входной области после 25 итераций обучения:

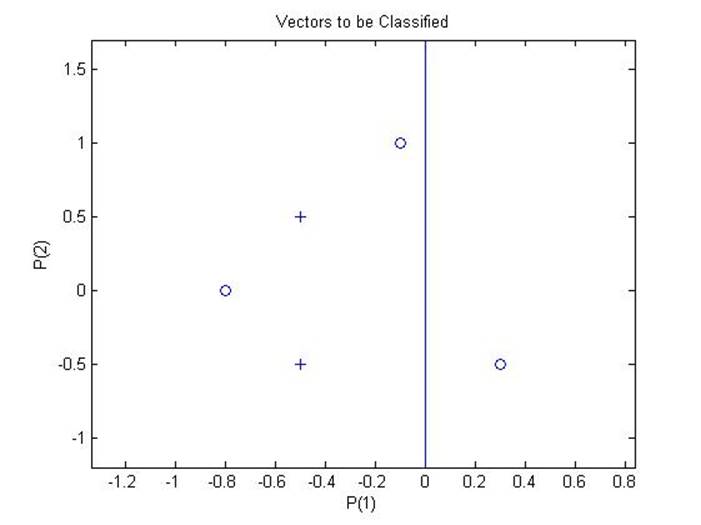
Как видно из графика, обучение попросту не может закончиться из-за линейной неотделимости входных векторов.

2.3. Линейные сети

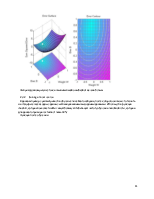
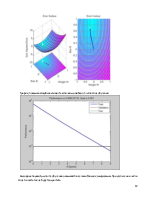
2.3.1.  Pattern association showing error surface