Возможности среды Matlab для построения нейронных сетей, использование предоставленными возможностями, страница 3

Один из методов улучшения обобщения сети – это использование сети достаточно большой для обеспечения адекватного соответствия. Однако, заранее довольно сложно предугадать, насколько большая сеть может понадобиться.

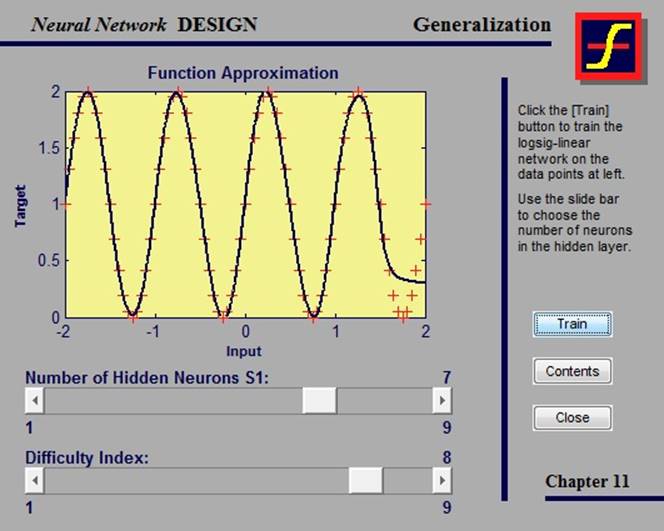
Следует заметить, что, если количество параметров в сети гораздо меньше, чем общее количество точек в обучающем  наборе, то шанс переоценки мал либо вообще отсутствует.

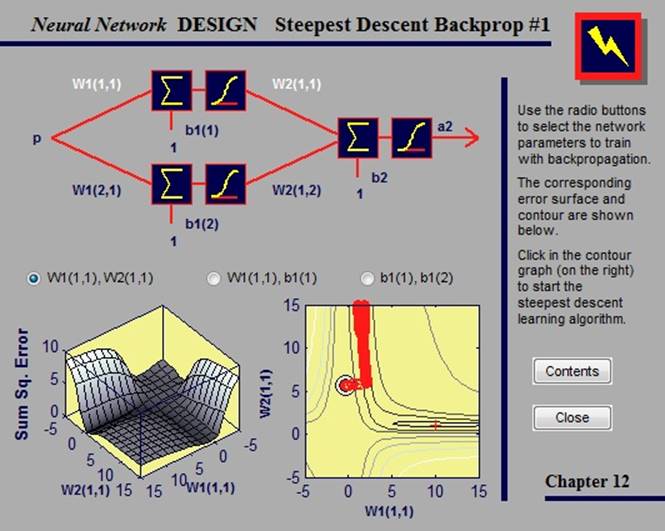
2.4.2.  Steepest descent backpropagation

В данном примере рассматривается алгоритм обучения, который сходится от десяти до ста раз быстрее, чем алгоритмы градиентного спуска.

Выбрав параметры сети, которые мы хотим обучить, и указав на появившемся контурном графе точку, мы инициируем обучающий алгоритм наискорейшего спуска.

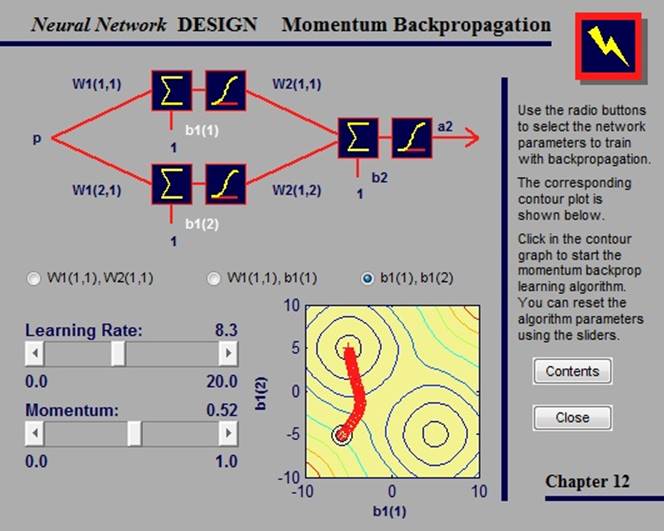
2.4.3.  Momentum backpropagation

Градиентный спуск с импульсом позволяет сети реагировать не только на локальный градиент, но и на последние тенденции в поверхности ошибок.

В данном примере мы можем проводить обучение сети, выбрав параметры, которые хотим обучить, и указав точку на контурном графе. Помимо этого, мы можем изменить параметры алгоритма, такие как коэффициент обучения и импусьс, сдвигая ползунки.

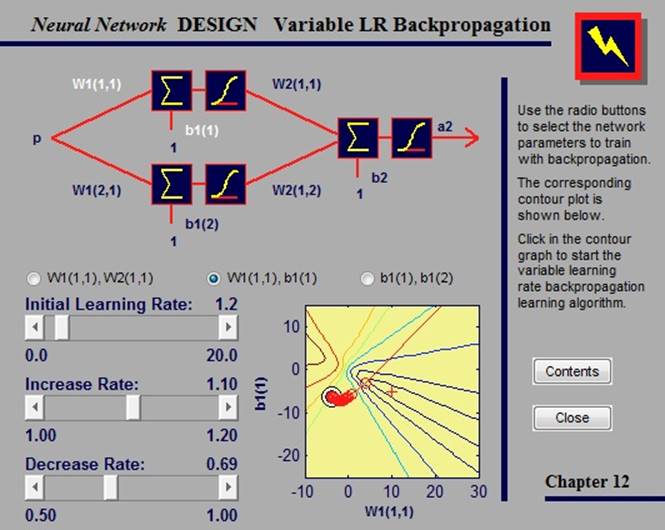
2.4.4.  Variable learning rate backpropagation

В стандартном алгоритме наискорейшего спуска коэффициент обучения остается постоянным на всем протяжении обучения. Но работа алгоритма очень чувствительна к величине коэффициента: если он слишком велик, алгоритм может стать нестабильным.

Улучшить алгоритм наискорейшего спуска можно, если разрешить коэффициенту обучения изменяться во время работы алгоритма. Адаптивный коэффициент стремится держать величину шага как можно большей, сохраняя при этом стабильность обучения.

В данном примере мы можем проводить обучение сети, выбрав параметры, которые хотим обучить, и указав точку на контурном графе. Помимо этого, мы можем изменить параметры алгоритма, такие как начальный коэффициент обучения, а также его увеличение и уменьшение, сдвигая ползунки.

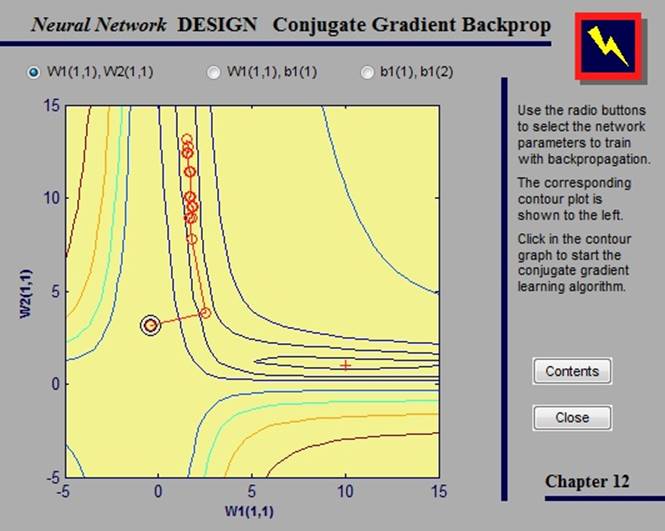
2.4.5.  Conjugate gradient backpropagation

Базовый алгоритм обратного распространения увеличивает вес направления наискорейшего спуска. В алгоритмах сопряженных градиентов поиск проводится по сопряженным направлениям, которые предлагают более быструю сходимость, чем направления наискорейшего спуска.

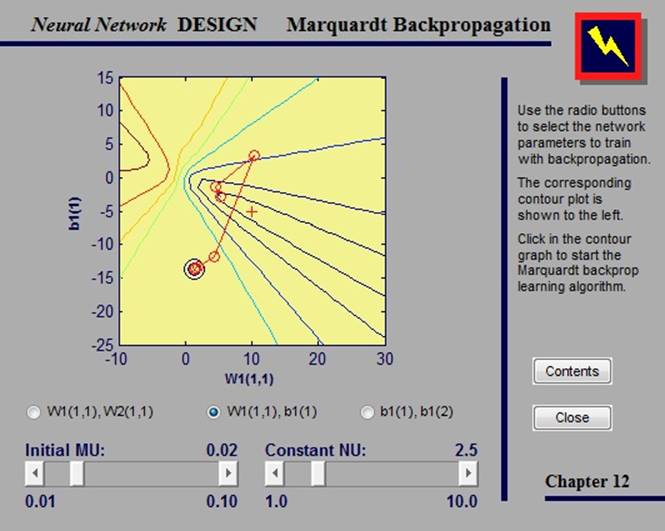
2.4.6.  Marquart-Levenberg backprogrammation

Как и квазиньютоновские методы, алгоритм Маркуарта-Левенберга был разработан для приближения к скорости обучения второго порядка без вычисления матрицы Гессе.

В данном примере мы можем проводить обучение сети, выбрав параметры, которые хотим обучить, и указав точку на контурном графе. Помимо этого, мы можем изменить параметры алгоритма, сдвигая ползунки.

2.5. Сети с радиальным базисом

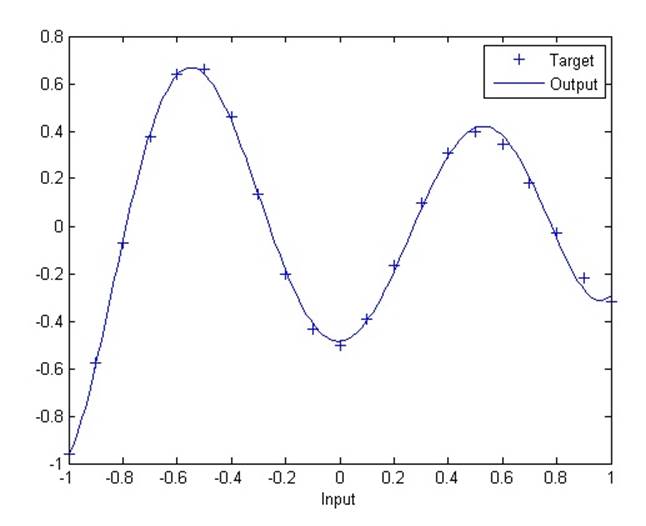
2.5.1.  Radial basis approximation

В данной демонстрации используется функция newrb, которая создает сеть с радиальным базисом для аппроксимации функции, заданной набором точек. В дополнение к обучающему набору и целевым показателям, функция требует еще два аргумента: допустимую ошибку и константу распространения.

2.5.2.  Radial basis underlapping neurons

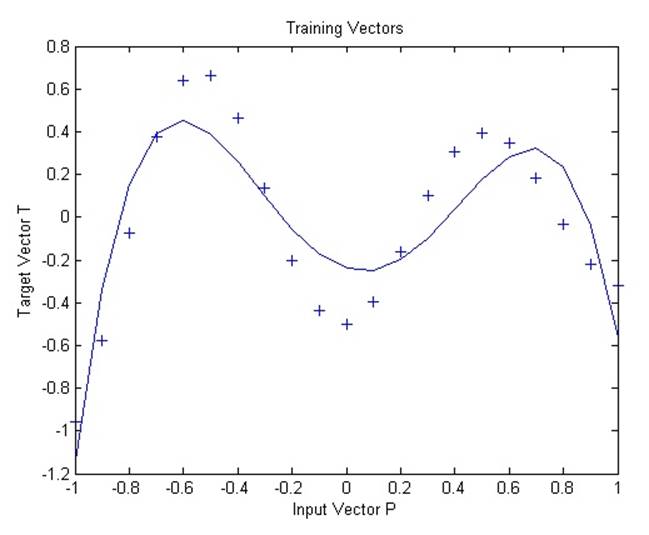
Сеть с радиальным базисом обучается реагировать на специфические входные данные запланированными выходными данными. Однако, поскольку распространение нейронов данной сети является крайне слабым, сети требуется большое количество нейронов.

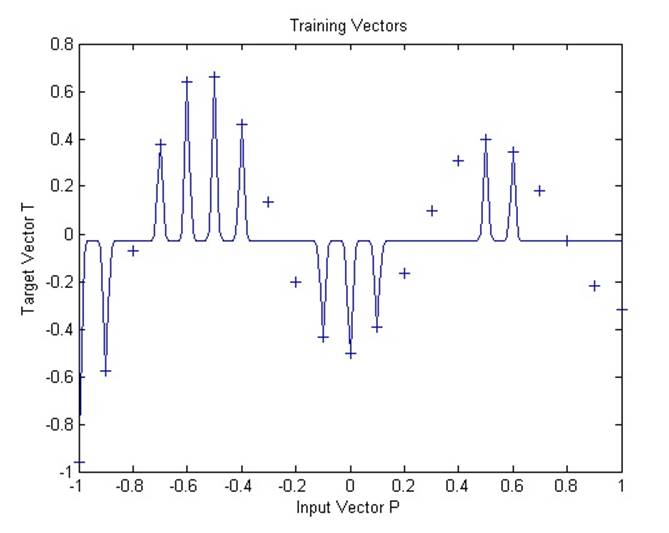
На графике становится видно, что функция была переопределена. Результат мог бы быть лучше с более высокой константой распространения.

2.5.3.  Radial basis overlapping neurons

Сеть с радиальным базисом обучается реагировать на специфические входные данные запланированными выходными данными. Однако, поскольку распространение нейронов данной сети является слишком высоким, каждый нейрон, по сути, возвращают одинаковые значения, и сеть не может быть спроектирована.

Все нейроны всегда возвращают единицу и не могут быть использованы, чтобы возвращать другие значения.

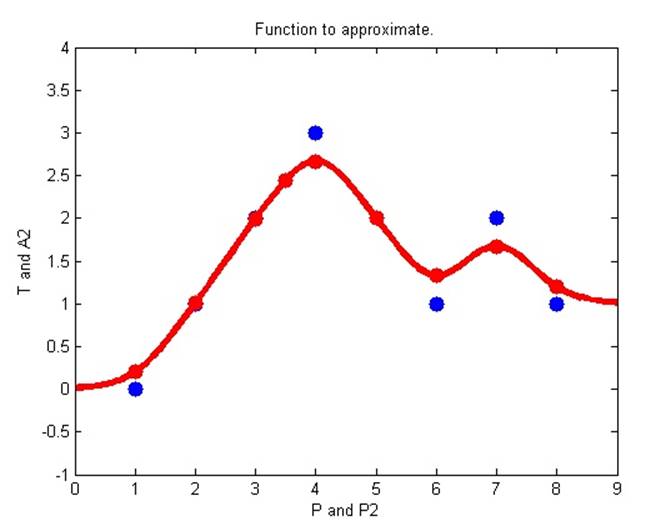
2.5.4.  GRNN function approximation

В данной демонстрации мы используем функцию newgrnn для того, чтобы создать обобщенную сеть регрессии. Мы можем использовать данную сеть, чтобы аппроксимировать функцию с новыми входными значениями.

2.5.5.  PNN classification