Возможности среды Matlab для построения нейронных сетей, использование предоставленными возможностями, страница 2

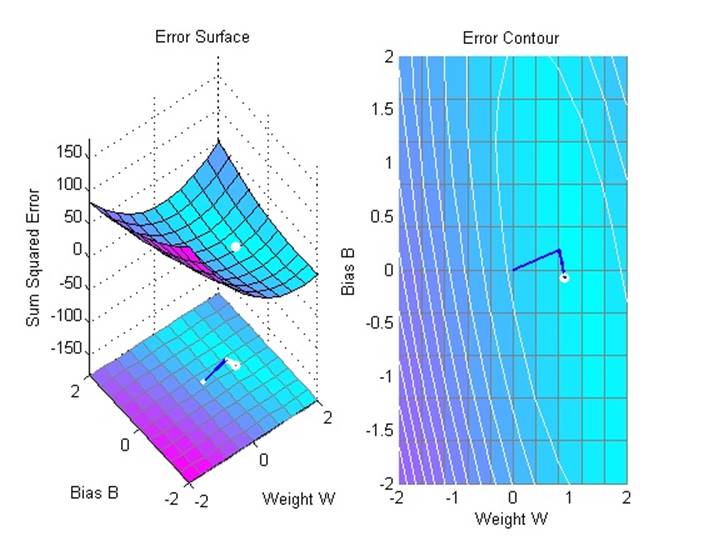
Линейный нейрон спроектирован, чтобы отвечать на специфические входные данные запланированными выходными данными. В примере используется функция errsurf, которая рассчитывает ошибки для нейрона с учетом возможного веса и значений порога и функция plotes, которая делает график полученной поверхности поверх контурного графика. Наилучшие значения веса и порога имеет нижайшая точка поверхности.

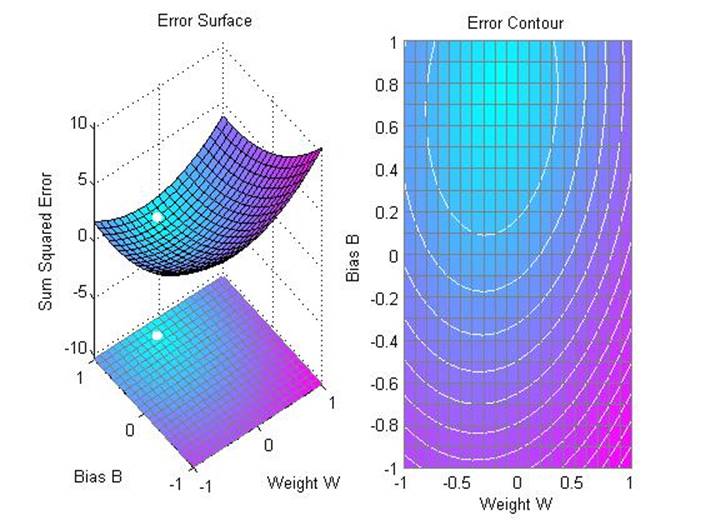
На приведенном рисунке точка с минимальной ошибкой отмечена белым

2.3.2.  training a linear neuron

В данном примере рассматривается обучение линейного нейрона, после которого он сможет отвечать на специфические входные данные запланированными выходными данными. Используется функция maxlinlr, которая позволяет найти самую большую стабильную частоту обучения линейной сети, которая для данного примера составляет лишь 40%.

Функция после обучения:

 

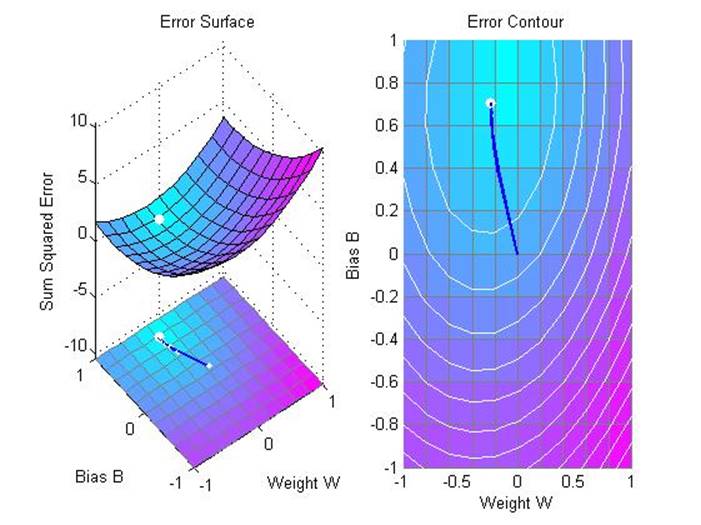
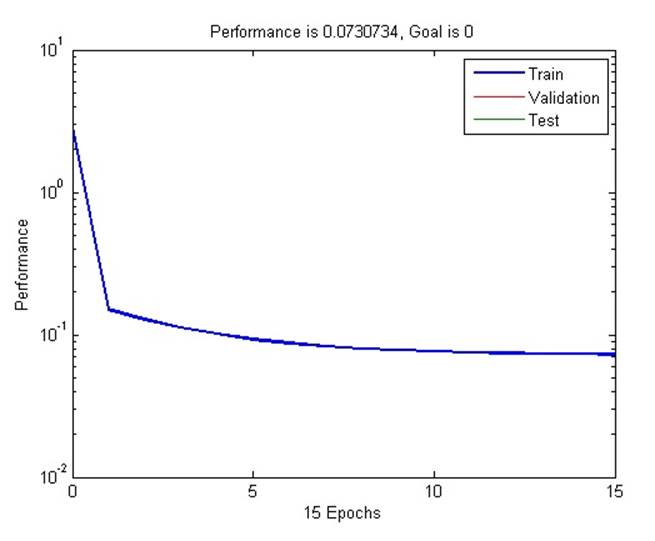
График, показывающий зависимость величины ошибки от числа эпох обучения:

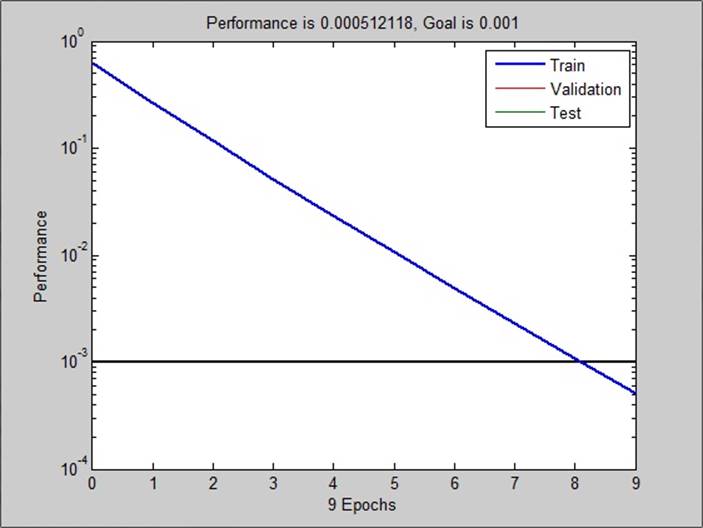
Выходные параметры после обучения оказываются весьма близки к ожидаемым. При увеличении числа эпох точность также будет возрастать.

2.3.3.  Linear classification system

Линейная сеть может быть обучена, чтобы выполнять линейную классификацию, при помощи функции train. Эта функция рассматривает каждый вектор из набора входных векторов и вычисляет вес сети и порог шага, причитающийся каждому из входов. Данный пример демонстрирует, как сеть может быть обучена, чтобы классифицировать различные образцы, и показывает, как обученная нейронная сеть действует, когда присутствуют зашумленные образцы.

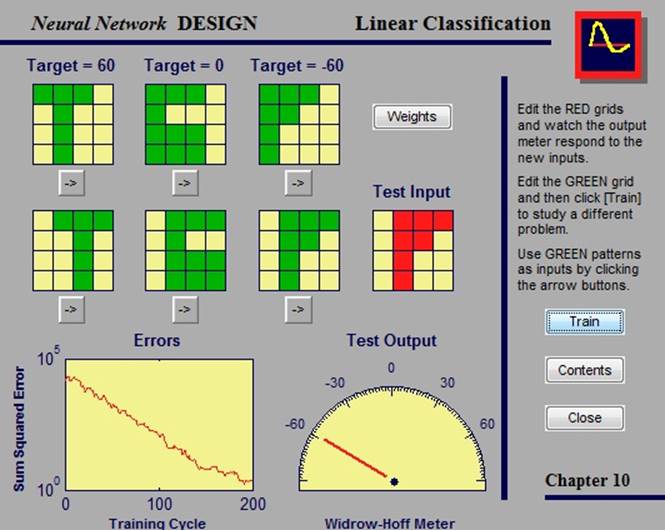
2.3.4. Adaptive noise cancellation

В подавлении шума при помощи адаптивных фильтров появляется возможность убрать посторонние шумы из сигнала в режиме реального времени. Сигнал, подлежащий очистке, содержит в себе шумы и требуемую информацию. Чтобы избавиться от шума, необходимо пропустить сигнал через адаптивный фильтр, который представляет шум, который коррелирует с шумом, который необходимо убрать из исходного сигнала.

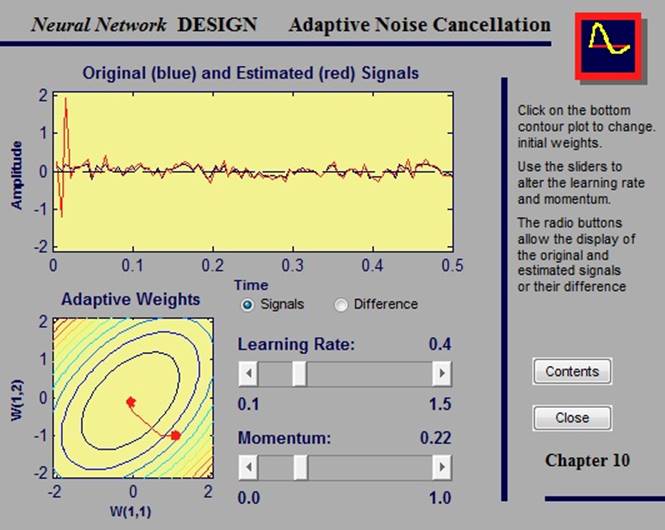
2.3.5. Adaptive noise cancellation in airplane

Представим пилота в самолете. Когда он говорит по рации, шум двигателей, присутствующий в кабине, накладывается на голосовой сигнал. Этот дополнительный шум сильно снижает качество итогового сигнала, который слышат пассажиры. Цель - выделить сигнал, содержащий голос пилота, но не шум двигателей. Сделать это можно, пропустив сигнал через один из адаптивных фильтров.

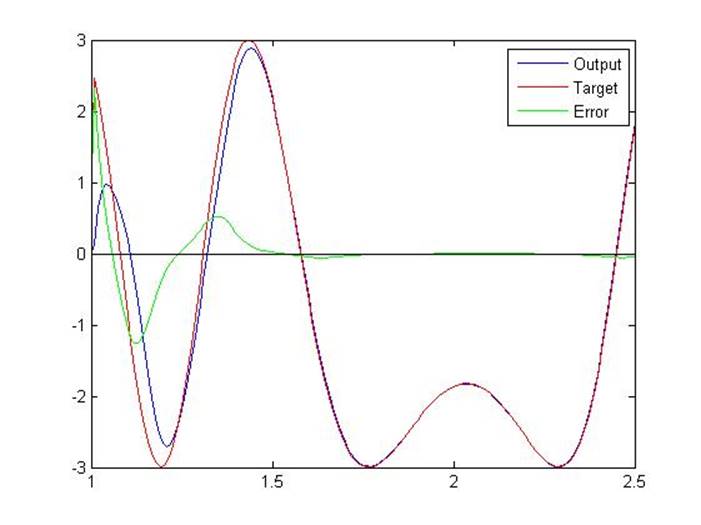
2.3.6. Linear fit of nonlinear problem

Линейный нейрон обучается находить минимальную ошибку, линейно подходящую к нелинейной проблеме. Следует отметить, что, поскольку проблема нелинейна, нулевая ошибка невозможна.

2.3.7. Undetermined problem

Линейный нейрон обучается находить неуникальные решения неопределенной проблемы.

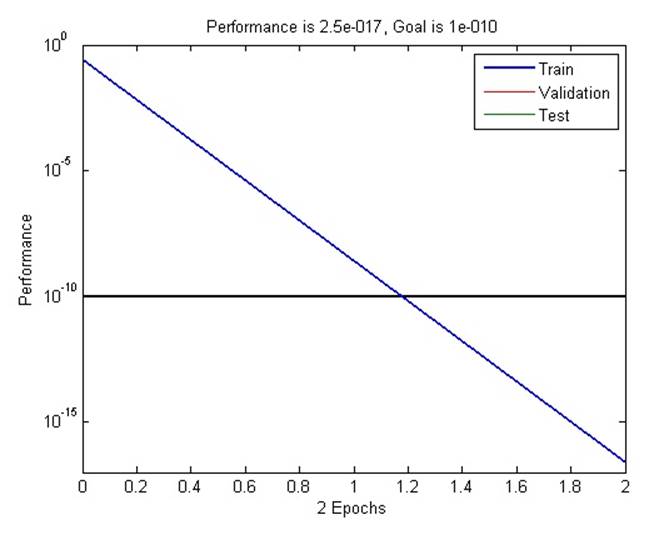
Выходные данные функции обучения – обученная сеть и история обучения. На следующем рисунке ошибки построены соответственно эпохам обучения.

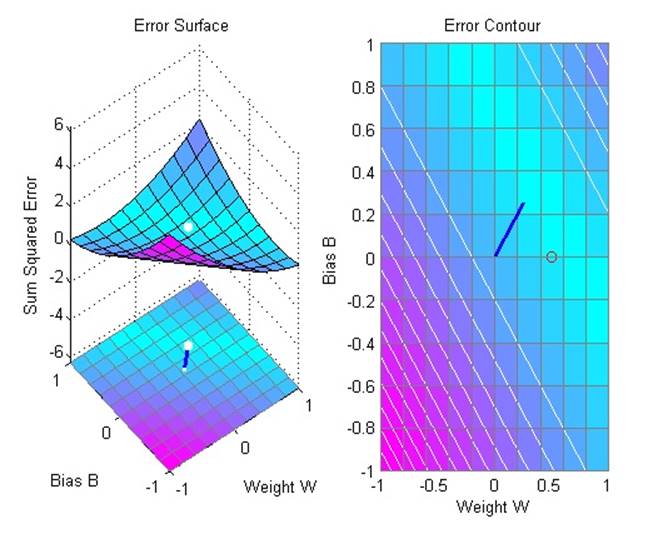
Поскольку проблема не определена, представленное решение не уникально.

2.3.8. Linearly dependent problem

Линейный нейрон обучается находить решение с минимальной ошибкой для проблемы с линейно зависимыми входными векторами. Если линейная зависимость входных векторов не соблюдается в полученных векторах, то проблема нелинейна и не имеет решения с нулевой ошибкой.

>> P = [ 1.0   2.0   3.0;   4.0   5.0   6.0];

>> T = [0.5 1.0 -1.0];

>> maxlr = maxlinlr(P,'bias');

>>net = newlin([0 10;0 10],1,[0],maxlr);

>> net.trainParam.show = 50;

>>net.trainParam.epochs = 500;

>>net.trainParam.goal = 0.001;

>> [net,tr] = train(net,P,T);

>> p = [1.0; 4];

a = sim(net,p)

a =

0.8971

2.3.9. Too large a learning rate

Линейный нейрон обучается находить решение с минимальной ошибкой для простой проблемы. Нейрон обучается с коэффициентом обучения большим, нежени предлагает функция maxlinlr.

Выходные данные функции обучения – обученная сеть и история обучения. На следующем рисунке ошибки построены соответственно эпохам обучения.

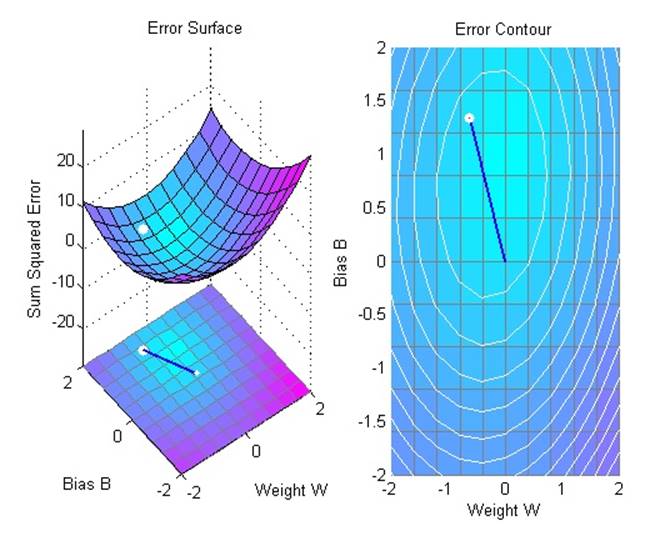
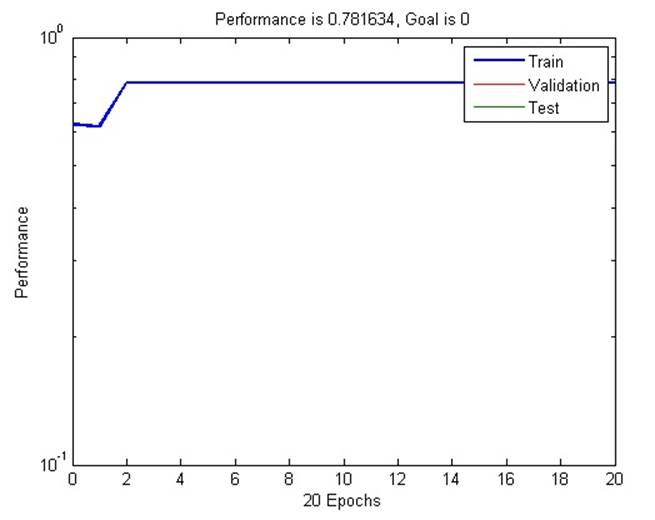
2.4. Метод обратного распространения ошибки

2.4.1.  Generalization

Одна из проблем, которая возникает во время обучения нейронной сети – это переоценка. Ошибка обучения сводится к очень малому значению, но, когда в сеть вносятся новые данные, - ошибка велика. Сеть запоминает обучающие примеры, но не обучена распространять их на новые ситуации.