Возможности среды Matlab для построения нейронных сетей, использование предоставленными возможностями, страница 4

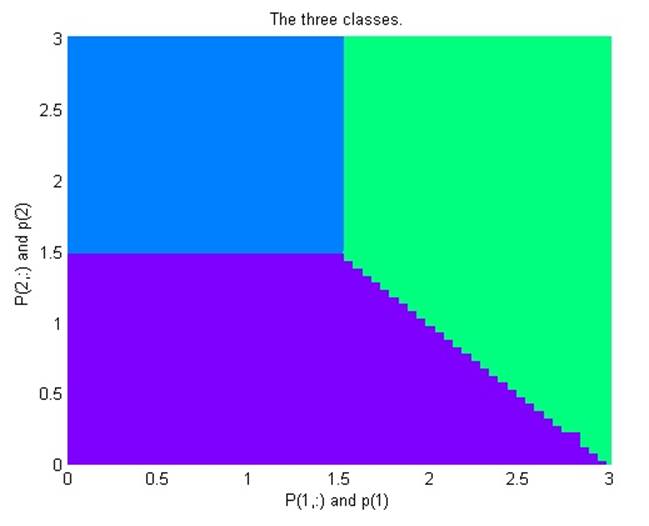
Мы имеем три двухэлементных входных вектора и ассоциированные с ними классы. Нам необходимо создать вероятностную нейронную сеть, которая правильно классифицирует эти векторы. Для этого сперва необходимо конвертировать классы в векторы, а затем создать вероятносную сеть и провести симуляцию. Затем, по результатам, строится диаграмма, показывающая, как вероятностная нейронная сеть делит входное пространство на три класса.

2.6. Самоорганизующиеся сети

2.6.1.  Competitive learning

Нейроны в соревновательном слое распределяют себя для распознавания часто встречающихся входных векторов. Чтобы классифицировать эти точки на естественные классы используется соревновательная сеть.

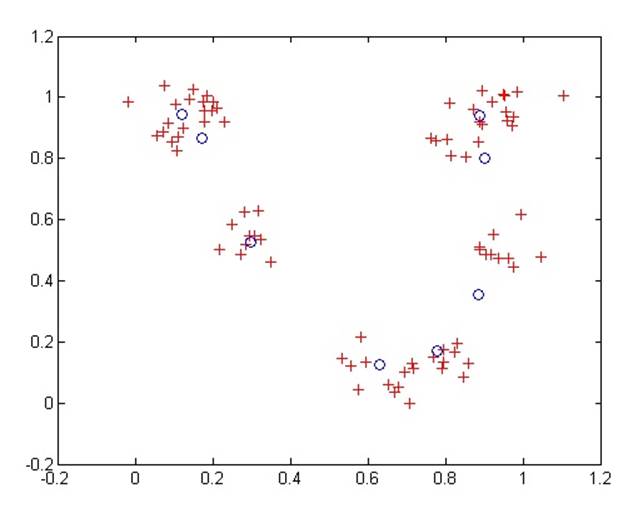
Синие круги – векторы веса, которые позволяют увидеть первоначальные попытки классификации.

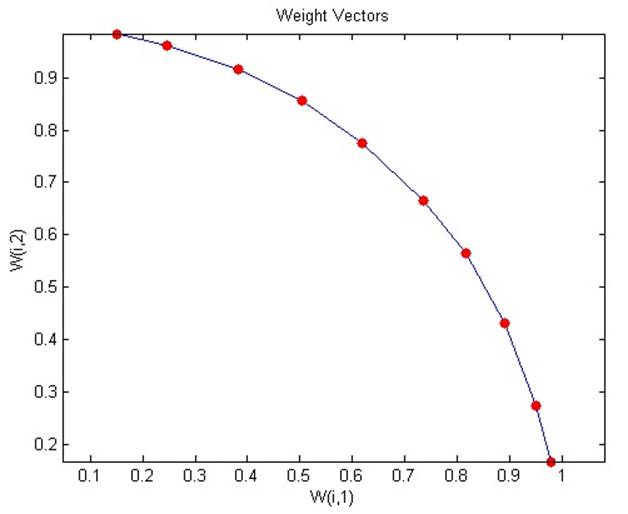
2.6.2.  One-dimensional self-organizing map

Как и в случае с соревновательными слоями, нейроны самоорганизующейся карты будут располагать себя с примерно равными расстояниями между собой, если входные векторы появляются с равной частотой в секции входного пространства. Если входные вектора появляются с разной частотой по входному пространству, то выбранный слой карты стремится расположить нейроны по пространству пропорционально частоте появления там входных векторов.

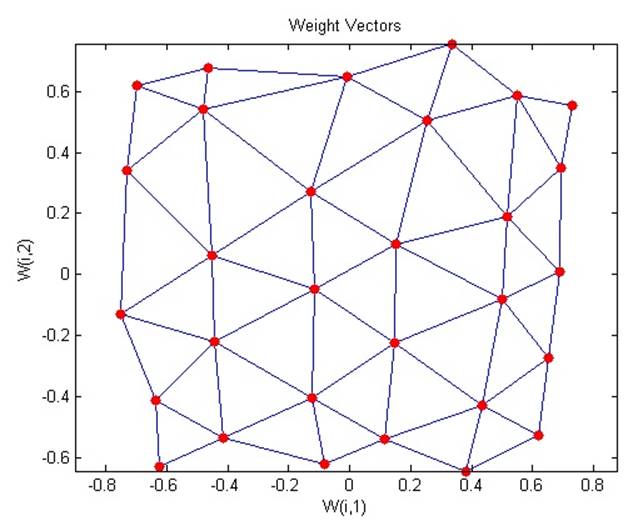
2.6.3.  Two-dimensional self-organizing map

Эта самоорганизующаяся карта обучается представлять различные участки входного пространства, в которых присутствуют входные вектора. Однако в данной демонстрации нейроны будут располагать себя в двумерную решетку, а не в линию.

2.7. Сети квантования обучающего вектора

2.7.1.  Learning vector quantization

Сети квантования обучающего вектора обучаются классифицировать входные вектора по заданным условиям. В качестве входных данных используются двухэлементные векторы и классы, на которые делятся эти векторы. Заданные классы можно трансформировать в вектора, чтобы использовать их в качестве условий.

newlvq создает слой квантования обучающего вектора. После получившуюся сеть необходимо обучить, для чего сперва необходимо отменить стандартное количество эпох.

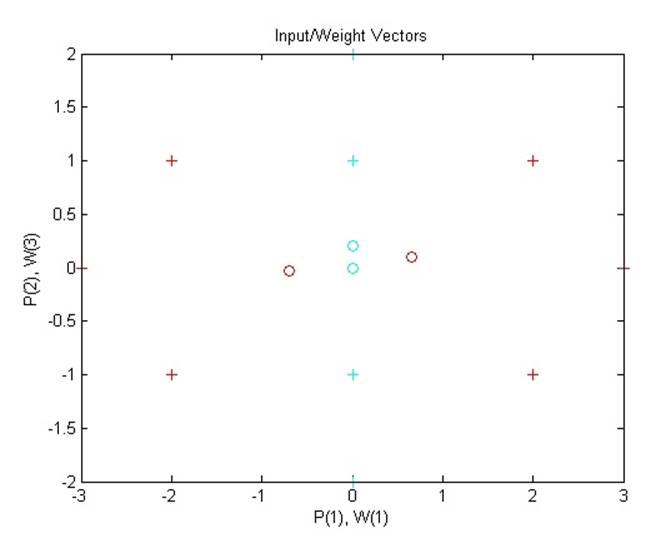
Красные точки – класс 1; голубые – класс 2.

При проведении симуляции:

p = [0.2; 1];

a = vec2ind(sim(net,p))

a =

2

2.8. Сети Хопфилда

2.8.1.  Hopfield two neuron design

Сеть Хопфилда, состоящая из двух нейронов, имеет две точки стабильного равновесия.

Нам необходимо получить сеть Хопфилда, которая имеет две стабильные точки, определенные двумя векторами условий.

Сеть Хопфилда создается при помощи функции hewhop. Для проверки стабильности векторов условий мы передаем их в сеть Хопфилда. В случае успеха они будут возвращены без изменений.

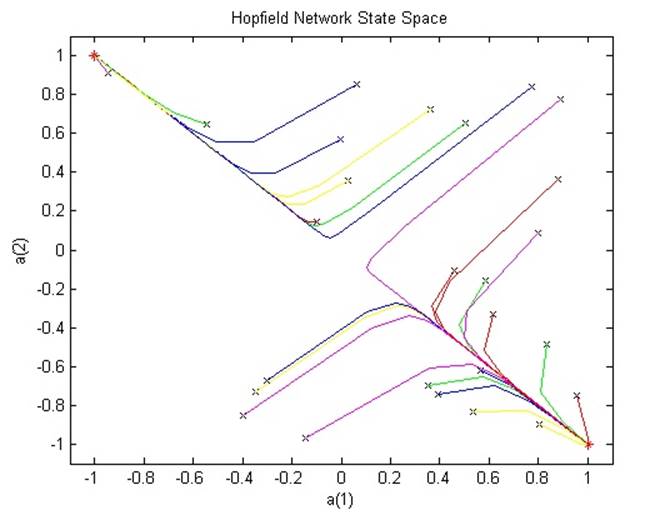
Следует отметить, что, если сеть стартует ближе к левой верхней точке, то закончит она именно в ней. И наоборот.

2.8.2.  Hopfield unstable equilibria

Сеть Хопфилда спроектирована с целевыми стабильными точками. Однако, несмотря на то, что newhop находит решение с минимальным числом неопределенных стабильных точек, зачастую они все же появляются. Сеть Хопфилда, спроектированная в данном примере, имеет нежелательную точку равновесия. Однако такие точки нестабильны и любой шум в системе выведет сеть из них.

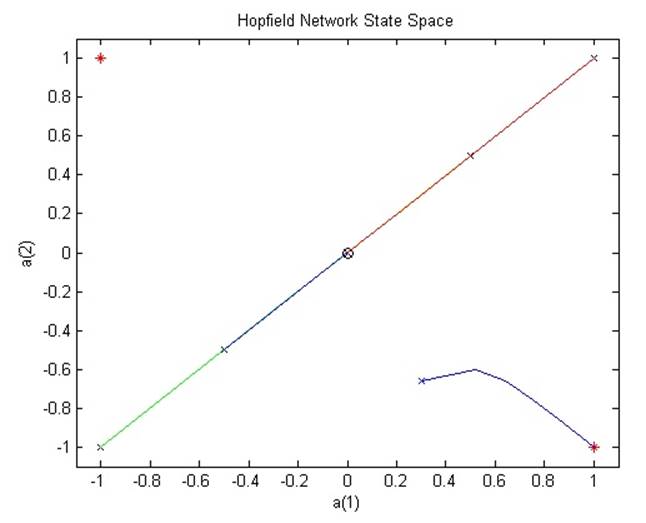
Как видно из графика, в данном примере нежелательные точки расположены прямо посередине между целевыми стабильными точками.

2.8.3.  Hopfield three neuron design

Сеть Хопфилда спроектирована с целевыми стабильными точками. Изучается поведение сети Хопфилда для других начальных условий.

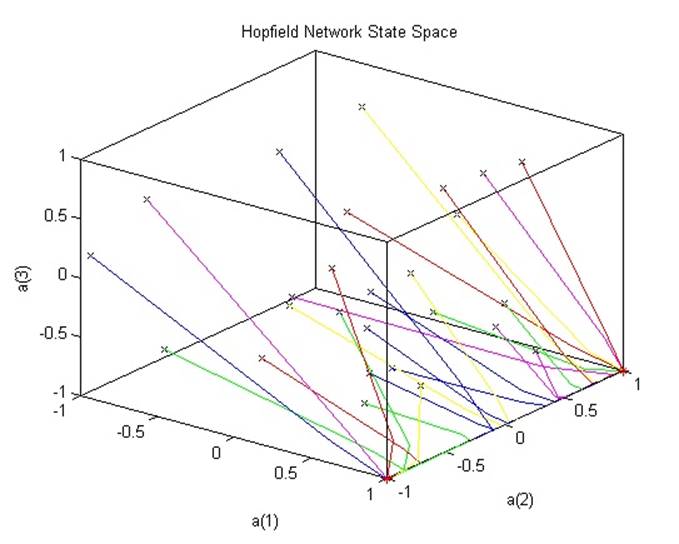
При проверке стабильности векторов условий, как видно на рисунке сверху, сеть оканчивает работу в указанных точках.

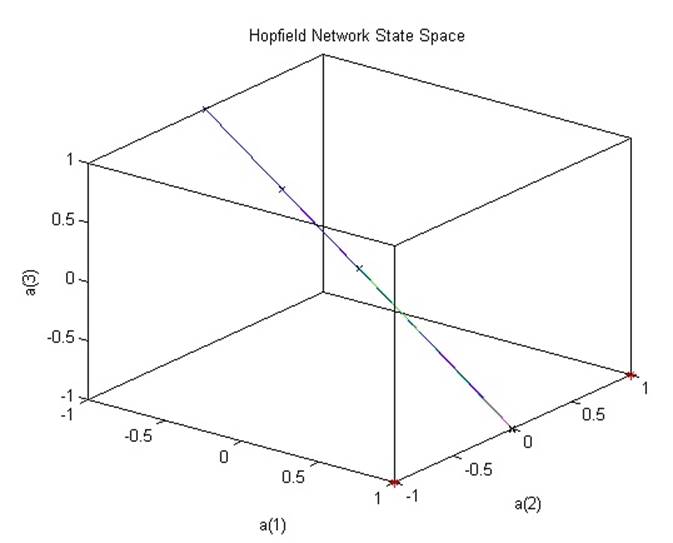
Нежелательные стабильные точки находятся ровно посередине между целевыми стабильными точками, что подтверждает рисунок, приведенный выше.

2.8.4.  Hopfield spurious stable points

Сеть Хопфилда с пятью нейронами спроектирована таким образом, чтобы иметь четыре стабильных равновесия. Однако она все равно будет иметь другие, нежелательные равновесия.

Цель примера – получить сеть Хопфилда с четырьмя стабильными точками, определенными при помощи двух целевых векторов.

T = [+1 +1 -1 +1; ...

-1 +1 +1 -1; ...

-1 -1 -1 +1; ...

+1 +1 +1 +1; ...

-1 -1 +1 +1];

net = newhop(T);