Возможности среды Matlab для построения нейронных сетей, использование предоставленными возможностями, страница 6

pause % Strike any key to design the network...

%    DEFINE THE NETWORK

%    ==================

%    NEWLIN generates a linear network.

%    We will use a learning rate of 0.1, and five

%    delays in the input.  The resulting network

%    will predict the next value of the target signal

%    using the last five values of the target.

lr = 0.1;

delays = [1 2 3 4 5];

net = newlin(P,1,delays,lr);

pause % Strike any key to adapt the linear neuron...

%    ADAPTING THE LINEAR NEURON

%    ==========================

%    ADAPT simulates adaptive linear neurons.  It takes the initial

%    network, an input signal, and a target signal,

%    and filters the signal adaptively.  The output signal and

%    the error signal are returned, along with new network.

%    Adapting begins...please wait...

[net,y,e]=adapt(net,P,T);

%    ...and finishes.

pause % Strike any key to see the output signal...

%    PLOTTING THE OUTPUT SIGNAL

%    ==========================

%    Here the output signal of the linear neuron is plotted

%    with the target signal.

plot(time,cat(2,y{:}),time,cat(2,T{:}),'--')

xlabel('Time');

ylabel('Output ---  Target - -');

title('Output and Target Signals');

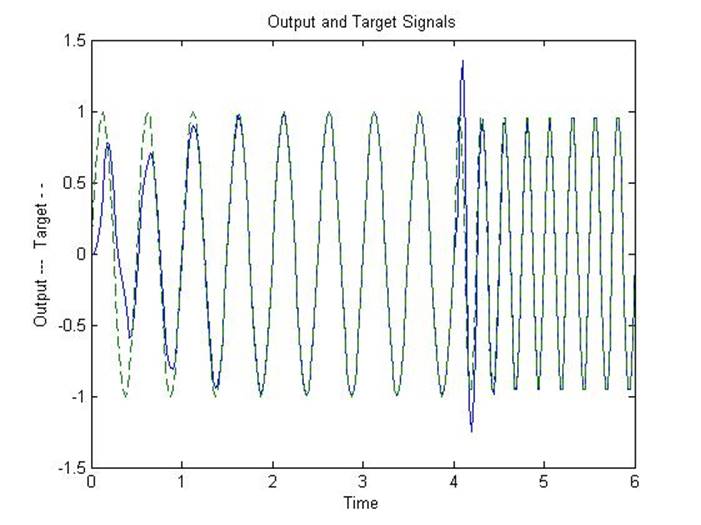
%    It does not take the adaptive neuron long to figure out

%    how to generate the target signal.

pause % Strike any key to see the error signal...

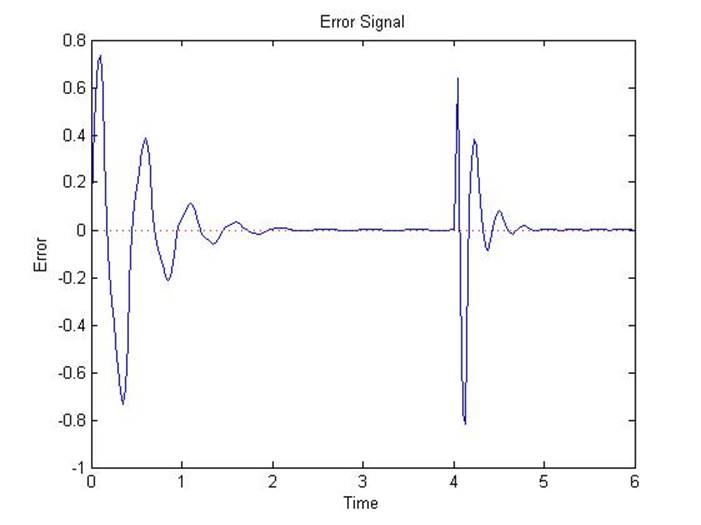
%    A plot of the difference between the neurons output

%    signal and the target signal shows how well the

%    adaptive neuron works.

plot(time,cat(2,e{:}),[min(time) max(time)],[0 0],':r')

xlabel('Time');

ylabel('Error');

title('Error Signal');

echo off

End of APPLIN2

2.9.3.  Elman amplitude detection

Сети Эльмана могут быть обучены распознавать и воспроизводить как пространственные, так и временные структуры. Примером задачи, в которой временные структуры распознаются и сопоставляются с пространственной структурой является обнаружение амплитуды.

Распознавание амплитуды требует, чтобы сигнал был представлен во времени, а также, чтобы на выходе сети была амплитуда сигнала. Это несложная проблема, но она иллюстрирует процесс проектирования сети Эльмана.

%    NEWELM  - Inititializes an Elman recurrent network.

%    SIM   - Simulates an Elman recurrent network.

%    TRAIN - Trains an Elman recurrent network.

%    AMPLITUDE DETECTION:

%    Using the above functions an Elman network is trained

%    to output the amplitude of a sine wave being presented

%    in time.

pause % Strike any key to continue...

%    DEFINING THE PROBLEM

%    ====================

%    The first wave form has an amplitude of 1.

p1 = sin(1:20);     % If input is wave with amplitude of 1

t1 = ones(1,20);    % then output should be 1

%    The second wave form has an amplitude of 2.

p2 = sin(1:20)*2;   % If input is wave with amplitude of 2

t2 = ones(1,20)*2;  % then output should be 2

%    The network will be trained on the sequence formed by

%    repeating each wave form twice.

p = [p1 p2 p1 p2];

t = [t1 t2 t1 t2];

Pseq = con2seq(p);

Tseq = con2seq(t);

pause % Strike any key to define the Elman network...

% DEFINE THE EHLMAN NETWORK

% =========================

%    The function NEWELM creates an Elman network whose input

%    varies from -2 to 2, and has 10 hidden neurons and 1 output.

net = newelm([-2 2],[10 1],{'tansig','purelin'},'traingdx');

Warning: NEWELM used in an obsolete way.

> In nntobsu at 18

In newelm at 98

In appelm1 at 51

See help for NEWELM to update calls to the new argument list.

net.trainParam.epochs = 500;

net.trainParam.show = 5;

net.trainParam.goal = 0.01;

pause % Strike any key to train the Elman network...

%    TRAINING THE ELMAN NETWORK

%    ===========================

%    TRAIN trains Elman networks.  Here it is trained

%    without training parameters. (The default will be used.)

%    Training begins...please wait, this takes a while...

tic

[net,tr] = train(net,Pseq,Tseq);

toc

Elapsed time is 24.154738 seconds.

%    ...training done.

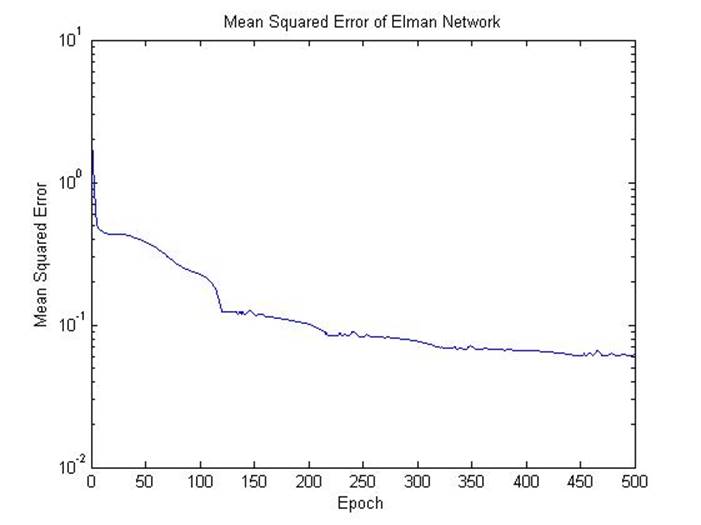
semilogy(tr.epoch,tr.perf)

title('Mean Squared Error of Elman Network')

xlabel('Epoch')

ylabel('Mean Squared Error')

pause % Strike any key to test the Elman network...