Санкт-Петербургский государственный политехнический университет
Факультет технической кибернетики
Кафедра
автоматики и вычислительной техники
РАСЧЕТНОЕ ЗАДАНИЕ №2
Дисциплина: Оптимальные системы управления
Тема: Расчет максимальной по быстродействию системы управления
Выполнила студентка гр. 5081/2
Руководитель
19 ноября 2009 г.
Санкт-Петербург 2009
Постановка задачи
Построить временные характеристики переменных состояния и фазовый портрет оптимальной по быстродействию системы для двух случаев:
— Ограничения наложены только на управление
— Ограничения наложены на управление и на переменные состояния.
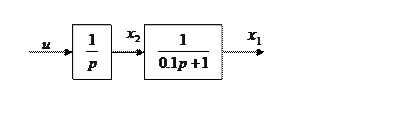
Рис.1.1 Структурная схема системы управления
Ограничения
на управление: 
.
Ограничения
на переменные состояния: 
Начальные
значения переменных состояния: 
, 
Конечные
значения переменных состояния:
,
1. Синтез оптимальной системы при ограничениях на управление
Заданная система описывается следующим образом:
;
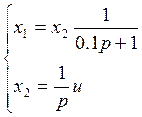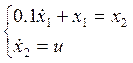(2.1)
Определим управляемость системы, для этого построим матрицу U и определим ее ранг:
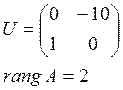
Таким образом, пара матриц А и В не вырождена и заданная система управляема.
Корни характеристического полинома отрицательны и вещественные (система устойчивая):
Таким образом,
заданная система удовлетворяет требованиям теоремы о 
–
интервалах. Оптимальное управление 
является
кусочно-постоянным и имеет не более двух интервалов постоянства. Управляющее
воздействие – 
(т.к. 
).
а) Система
(2.1) на первом участке (
) имеет вид:
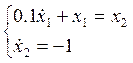(2.3)
Решим её с учетом начальных условий (, ):
>> U1=dsolve('0.1*Dx1+x1=x2,Dx2=-1','x1(0)=10,x2(0)=0', 't');
>> U1.x1
ans =
-t+1/10+99/10*exp(-10*t)
>> U1.x2
ans =
-t
>>
Таким образом, решение системы (2.3):
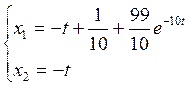(2.4)
б) Система
(2.1) на втором участке (
) имеет вид:
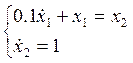(2.5)
Решим её:
>> U2=dsolve('0.1*Dx1+x1=x2,Dx2=1','t');
>> U2.x1
ans =
t-1/10+C2+exp(-10*t)*C1
>> U2.x2
ans =
t+C2
>>
Таким образом, решение системы (2.5) :
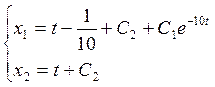(2.6)
в) Из систем
2.4-2.6 определим константы 
и 
, время переключения 
, время окончания управления 
:
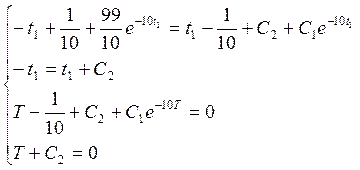
>> Res=solve('-t1+1/10+99/10*exp(-10*t1)=t1-1/10+C2+exp(-10*t1)*C1','-t1=t1+C2','tk-1/10+C2+exp(-10*tk)*C1=0','tk+C2=0');
>> Res.C1
ans =
81/10
121/10
>> Res.C2
ans =
-1/5*log(9)+1/5*i*pi
-1/5*log(11)
>> Res.t1
ans =
1/10*log(9)-1/10*i*pi
1/10*log(11)
>> Res.tk
ans =
1/5*log(9)-1/5*i*pi
1/5*log(11)
Таким образом, получили:
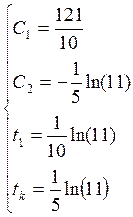
Уравнения переменных состояния (с учетом полученных параметров):
На первом участке:
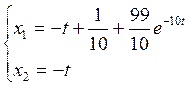
На втором участке:
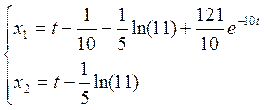
Построим временные характеристики переменных состояния и фазовый портрет (рис.2.1-2.3):
t_1=1/10*log(11)
t_2=1/5*log(11)
t1=[0:0.001:t_1];
t2=[t_1:0.001:t_2];
x11=-t1+1/10+99/10*exp(-10*t1);
x12=t2-1/10-1/5*log(11)+exp(-10*t2)*121/10;
x21=-t1;
x22=t2-1/5*log(11);
subplot(2,1,1);plot(t1,x11,t2,x12);grid on;hold on;
xlabel('t'); ylabel('X1'); title('X1 time response');
subplot(2,1,2);plot([0 t_1 t_1 t_2],[-1 -1 1 1]);grid on;
xlabel('t'); ylabel('U'); title('Optimal control');
figure
subplot(2,1,1);plot(t1,x21,t2,x22);grid on;hold on;
xlabel('t'); ylabel('X2'); title('X2 time response');
subplot(2,1,2);plot([0 t_1 t_1 t_2],[-1 -1 1 1]);grid on;
xlabel('t'); ylabel('U'); title('Optimal control');
figure
plot(x11,x21,x12,x22);grid on;hold on;
xlabel('X1'); ylabel('X2'); title('Phase portrait');
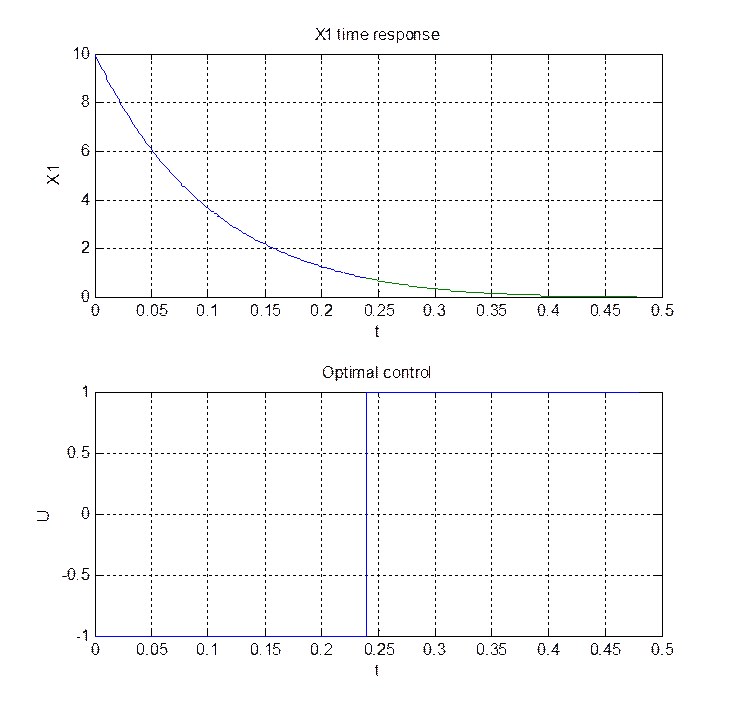
Рис.2.1.Временная характеристика переменной Х1
и оптимальное управление
Рис.2.2.Временная характеристика переменной Х2
и оптимальное управление
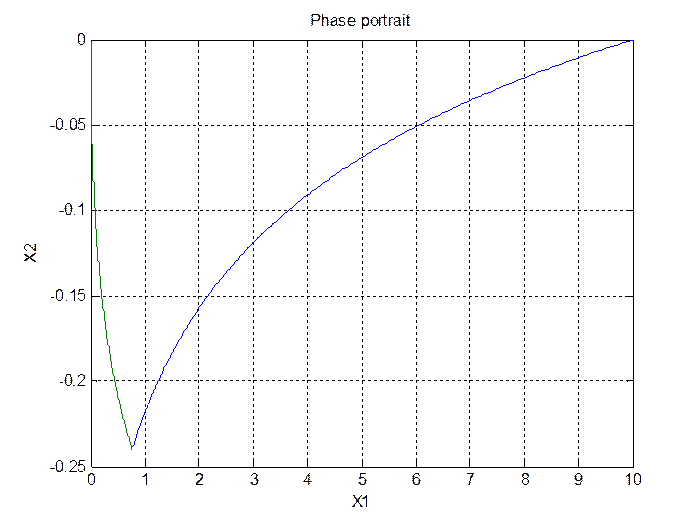
Рис.2.3.Фазовый портрет
2. Синтез оптимальной системы при ограничениях на управление и на переменные состояния
Ограничения
на управление: .
Ограничения
на переменные состояния:
Т.к. система
управления является линейной системой второго порядка, то управление будет
релейным с тремя участками переключения. а) Система
(2.1) на первом участке () имеет вид:
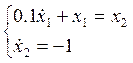(3.1)
Решим её с
учетом начальных условий (, ):
>> U1=dsolve('0.1*Dx1+x1=x2,Dx2=-1','x1(0)=10,x2(0)=0', 't');
>> U1.x1
ans =
-t+1/10+99/10*exp(-10*t)
>> U1.x2
ans =
-t
>>
Таким образом, решение системы (3.1):
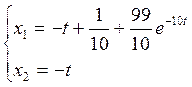(3.2)
б) Система
(2.1) на втором участке (
) имеет вид:
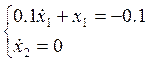(3.3)
Решим её:
>> U2=dsolve('0.1*Dx1+x1=-0.1,Dx2=0','t');
>> U2.x1
ans =
-1/10+exp(-10*t)*C1
>> U2.x2
ans =
C2
>>
Таким образом, решение системы (3.3) :
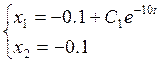(3.4)
в) Система
(2.1) на третьем участке () имеет вид:
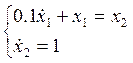(3.5)
Решим её:
>> U2=dsolve('0.1*Dx1+x1=x2,Dx2=1','t');
>> U2.x1
ans =
t-1/10+C2+exp(-10*t)*C1
>> U2.x2
ans =
t+C2
>>
Таким образом, решение системы (3.5):
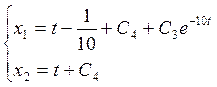(2.6)
г) Из систем 3.2,
3.4, 3.6 определим константы , 
, и 
,
времена переключения и 
,
время окончания управления :
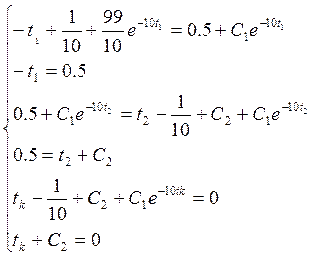
>>R=solve('-t1+1/10+99/10*exp(-10*t1)=-0.1+exp(-10*t1)*C1','-t1=-0.1','-0.1+exp(-10*t2)*C1=t2-1/10+C4+exp(-10*t2)*C3','-0.1=t2+C4','tk-1/10+C4+exp(-10*tk)*C3=0','tk+C4=0')
C1 =
10.171828182845904523536028747135
C3 =
16.091595251539168767386048798225
C4 =
-.50808821946113498088440118071996
t1 =
.10000000000000000000000000000000
t2 =
.40808821946113498088440118071996
tk =
.50808821946113498088440118071996
Уравнения переменных состояния (с учетом найденных параметров):
На первом участке:
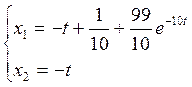
На втором участке:
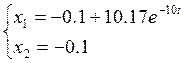
На третьем участке:
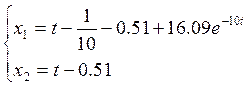
Построим временные характеристики переменных состояния и фазовый портрет (рис.3.1-3.3):
C1 =10.171828182845904523536028747135
C3 =16.091595251539168767386048798225
C4 =-.50808821946113498088440118071996
t1 =.10000000000000000000000000000000
t2 =.40808821946113498088440118071996
tk =.50808821946113498088440118071996
t_1=[0:0.001:t1];
t_2=[t1:0.001:t2];
t_3=[t2:0.001:tk];
x11 = -t_1+1/10+99/10*exp(-10*t_1)
x21 = -t_1
x12 = -1/10+exp(-10*t_2)*C1
x22 = -1/10
x13 = t_3-1/10+C4+exp(-10*t_3)*C3
x23 = t_3+C4
subplot(2,1,1);plot(t_1,x11,t_2,x12,t_3,x13);grid on;
xlabel('t'); ylabel('X1'); title('X1 time response');
subplot(2,1,2);plot([0 t1 t1 t2 t2 tk],[-1 -1 0 0 1 1]);grid on;
xlabel('t'); ylabel('U'); title('Optimal control');
figure
subplot(2,1,1);plot(t_1,x21,[t1 t2],[x22 x22],t_3,x23);grid on;
xlabel('t'); ylabel('X2'); title('X2 time response');
subplot(2,1,2);plot([0 t1 t1 t2 t2 tk],[-1 -1 0 0 1 1]);grid on;
xlabel('t'); ylabel('U'); title('Optimal control');
figure
plot(x11,x21,x12,x22,x13,x23);grid on;
xlabel('X1'); ylabel('X2'); title('Phase portrait');
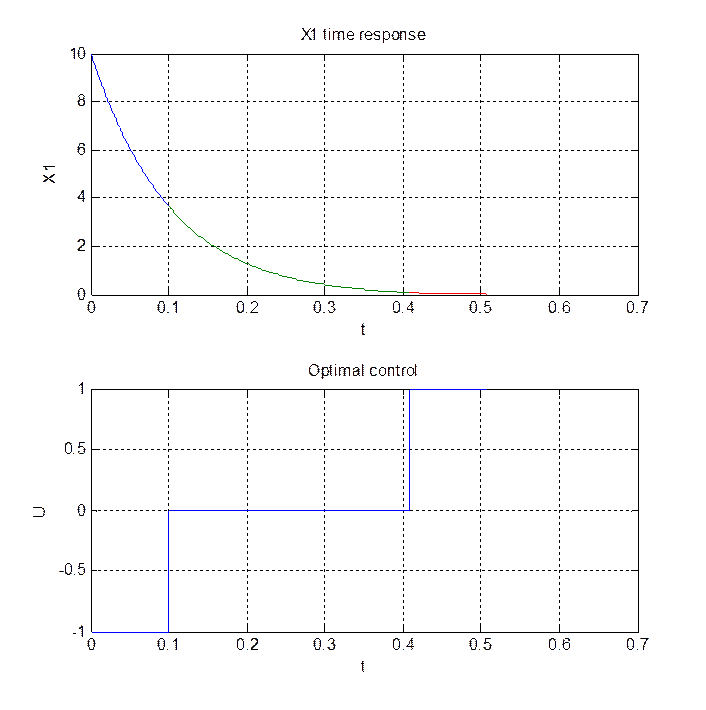
Рис.3.1.Временная характеристика переменной Х1
и оптимальное управление
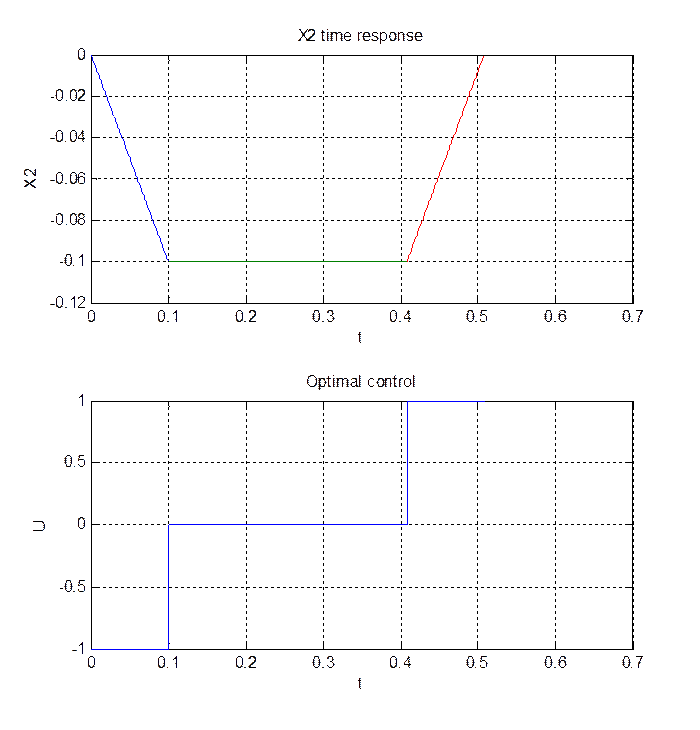
Рис.3.2.Временная характеристика переменной Х2
и оптимальное управление
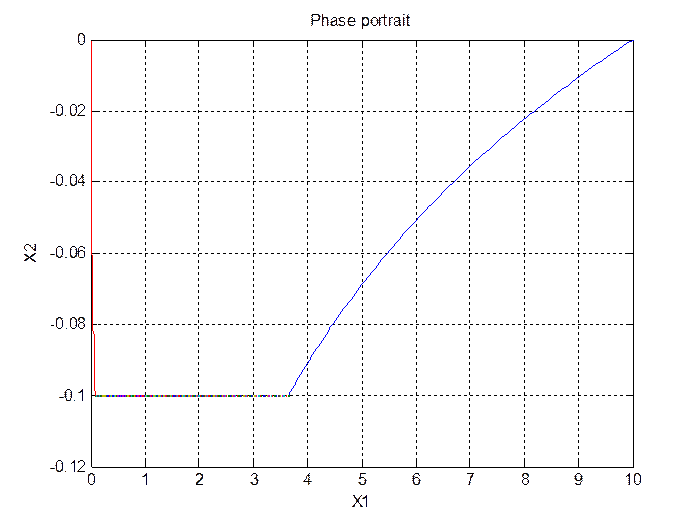
Рис.3.3.Фазовый портрет
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
