2.152. Дакажыце, што мнагасклад ![]() : а)
мае корань на адрэзку
: а)
мае корань на адрэзку ![]() ; б)
мае не менш трох рэчаісных каранёў.
; б)
мае не менш трох рэчаісных каранёў.
2.153. Дакажыце, што адвольны мнагасклад няцотнай ступені мае прынамсі адзін рэчаісны корань.
2.154. Няхай функцыі ![]() і
і ![]() непарыўныя на
адрэзку
непарыўныя на
адрэзку ![]() і
і ![]() , а
, а ![]() . Дакажыце, што
існуе пункт
. Дакажыце, што
існуе пункт ![]() такі, што
такі, што ![]() .
.
2.155. Няхай функцыі ![]() і
і ![]() непарыўныя на
адрэзку
непарыўныя на
адрэзку ![]() і мноства іх
значэнняў на гэтым адрэзку супадаюць. Дакажыце, што існуе, ва ўсякім разе,
адзін пункт
і мноства іх
значэнняў на гэтым адрэзку супадаюць. Дакажыце, што існуе, ва ўсякім разе,
адзін пункт ![]() такі, што
такі, што ![]() .
.
2.156. Дакажыце, што з раўнамернай непарыўнасці
функцый ![]() і
і ![]() на мностве
на мностве ![]() вынікае
раўнамерная непарыўнасць на гэтым мно-стве лінейнай камбінацыі
вынікае
раўнамерная непарыўнасць на гэтым мно-стве лінейнай камбінацыі ![]() пры адвольных
пры адвольных ![]() і
і ![]() .
.
2.157.
Карыстаючыся
азначэннем, дакажыце раўнамерную непарыўнасць функцыі ![]() на мностве
на мностве ![]() , калі:
1)
, калі:
1) ![]() ;
2)
;
2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
2.158. Дакажыце, што калі ![]() раўнамерна
непарыўная на адрэзках
раўнамерна
непарыўная на адрэзках ![]() і
і ![]() , то яна
раўнамерна непарыўная на адрэзку
, то яна
раўнамерна непарыўная на адрэзку ![]() .
.
2.159. Сфармулюйце ў дадатным сэнсе сцверджанне, што ![]() не з’яўляецца
раўнамерна непарыўнай на мностве
не з’яўляецца
раўнамерна непарыўнай на мностве ![]() .
.
2.160.
Дакажыце, што функцыя ![]() не з’яўляецца
раўнамерна непарыў-най на мностве
не з’яўляецца
раўнамерна непарыў-най на мностве ![]() калі:
1)
калі:
1) ![]() ; 2)
; 2) ![]()
2.161.
Даследуйце на
раўнамерную непарыўнасць на мностве ![]() функ-цыю
функ-цыю
![]() , калі: 1)
, калі: 1)![]() 2)
2)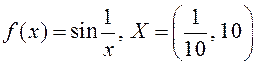 ;
3)
;
3)![]() ;
4)
;
4)![]() .
.
2.162. Дакажыце, што калі ![]() раўнамерна
непарыўная на інтэрвале
раўнамерна
непарыўная на інтэрвале ![]() ,
то існуюць наступныя ліміты:
,
то існуюць наступныя ліміты: ![]() і
і
![]() .
.
2.163. Дакажыце, што раўнамерна непарыўную на
інтэрвале ![]() функ-цыю можна
давызначыць у пунктах
функ-цыю можна
давызначыць у пунктах ![]() і
і ![]() так, што
функцыя будзе непарыўнай на адрэзку
так, што
функцыя будзе непарыўнай на адрэзку ![]() .
.
2.164. Дакажыце, што калі функцыя неабмежаваная на
канечным інтэрвале ![]() , то
яна не можа быць раўнамерна непарыўнай на гэтым інтэрвале.
, то
яна не можа быць раўнамерна непарыўнай на гэтым інтэрвале.
Няхай ![]() і
і ![]() вызначаны ў ваколлі
пункта а акрамя, можа
быць
вызначаны ў ваколлі
пункта а акрамя, можа
быць ![]() , прычым
, прычым ![]() і існуе
і існуе 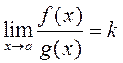 . Тады:
. Тады:
1) Калі ![]() , то
функцыю
, то
функцыю ![]() называюць бясконца
малой у параўнанні з функцыяй
называюць бясконца
малой у параўнанні з функцыяй ![]() пры
пры ![]() і пішуць:
і пішуць: ![]() . У
прыватнасці, запіс
. У
прыватнасці, запіс ![]() азначае,
што
азначае,
што ![]() , г. зн. што
, г. зн. што ![]() ёсць бясконца
малая функцыя пры
ёсць бясконца
малая функцыя пры ![]() .
Калі
.
Калі ![]() і
і ![]() пры
пры ![]() , то
, то ![]() называюць бясконца
малой больш высокага парадку, чым
называюць бясконца
малой больш высокага парадку, чым ![]() .
.
2) Калі ![]() ,
то функцыю
,
то функцыю ![]() называюць эквівалентнай
(або асімптатычна роўнаю) функцыі
называюць эквівалентнай
(або асімптатычна роўнаю) функцыі ![]() пры
пры ![]() і запісваюць:
і запісваюць: ![]() .
.
3) Калі ![]() і
і ![]() пры
пры ![]() , то іх
называюць бясконца малымі аднаго парадку пры
, то іх
называюць бясконца малымі аднаго парадку пры ![]() . У
прыватнасці,
. У
прыватнасці, ![]() называюць бясконца
малой
называюць бясконца
малой ![]() – га парадку
пры
– га парадку
пры ![]() , калі
, калі ![]() і
і ![]() з’яўляюцца
бясконца малымі аднаго парадку пры
з’яўляюцца
бясконца малымі аднаго парадку пры ![]() .
.
Аналагічна параўноваюцца бясконца вялікія функцыі.
Запіс ![]() ,
азначае, што існуе лік
,
азначае, што існуе лік ![]() ,
такі, што ў некаторым ваколлі пункта
,
такі, што ў некаторым ваколлі пункта ![]() .
.
Знаходжанне лімітаў функцый у многіх выпадках значна спрашчаецца, калі скарыстаць наступныя сцверджанні:
1) Калі
![]() і існуе
і існуе
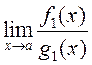 , то
, то 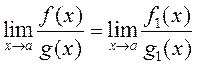 .
.
2) Крытэр
эквівалентнасці: ![]() калі
і толькі калі
калі
і толькі калі ![]() .
.
Асімптатычныя формулы пры ![]() :
:
![]() ,
,
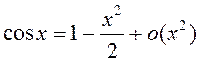 ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, 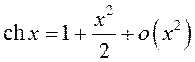 .
.
Гэтыя формулы застаюцца праўдзівымі пры ![]() , калі замест
аргумента
, калі замест
аргумента ![]() падставіць
бясконца малую пры
падставіць
бясконца малую пры ![]() функцыю
функцыю
![]() .
.
Прыклад 1. Даказаць, што ![]() .
.
►Няхай ![]() і
і ![]() пры
пры ![]() , г. зн.
, г. зн. 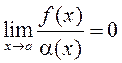 і
і 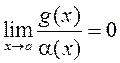 . Патрэбна
даказаць, што
. Патрэбна
даказаць, што ![]() або
або
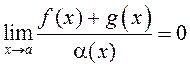 .
Сапраўды:
.
Сапраўды: 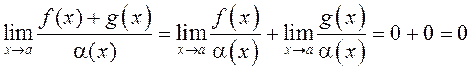 .◄
.◄
Прыклад 2. Даказаць, што ![]() .
.
► Няхай ![]() ,
а
,
а ![]() . Сцверджанне,
якое трэба даказаць, раўназначнае таму, што
. Сцверджанне,
якое трэба даказаць, раўназначнае таму, што ![]() (глядзі крэтыр
эквіва-лентнасці), або
(глядзі крэтыр
эквіва-лентнасці), або 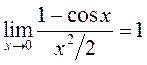 .
Сапраўды:
.
Сапраўды:
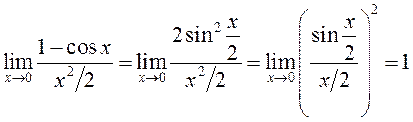 .◄
.◄
Прыклад 3. Знайсці 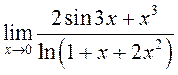 .
.
►Заўважым, што пры ![]()
![]() ,
, ![]() .
Выкарыстоўваючы крытэр эквівалентнасці, будзем мець:
.
Выкарыстоўваючы крытэр эквівалентнасці, будзем мець:
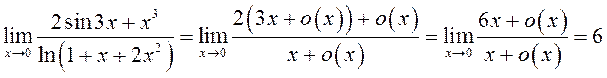 ,
(мы выкарысталі судачыненне
,
(мы выкарысталі судачыненне ![]() ).◄
).◄
Прыклад 4. Знайсці ![]() .
.
►З роўнасці ![]() і
непарыўнасці паказнікавай функцыі маем:
і
непарыўнасці паказнікавай функцыі маем: 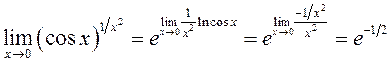 . ( Мы
скарысталі судачы-ненне:
. ( Мы
скарысталі судачы-ненне: ![]() .)
◄
.)
◄
2.165.
Ці будуць бясконца
малымі наступныя функцыі:
1) 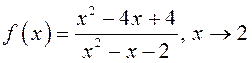 ; 2)
; 2) ![]() ;
3)
;
3) 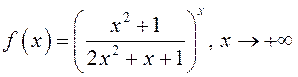 ; 4)
; 4) ![]() .
.
2.166.
Якія з наступных
функцый ёсць бясконца вялікія:
1) ![]() : а)
: а) ![]() , б)
, б) ![]() ;
2)
;
2) ![]() : а)
: а) ![]() , б)
, б) ![]() ;
3)
;
3) ![]() : а)
: а) ![]() б)
б) ![]() ?
?
2.167.
Падайце прыклады
бясконца малых пры ![]() функцый
функцый
![]() і
і ![]() такіх, што
такіх, што 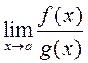 1) роўны 1; 2) роўны 0; 3) роўны ∞; 4)
не існуе.
1) роўны 1; 2) роўны 0; 3) роўны ∞; 4)
не існуе.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.