2.83.
Дакажыце, што паслядоўнасць ![]() будзе збежнай,
калі збягаюцца наступныя яе падпаслядоўнасці:
будзе збежнай,
калі збягаюцца наступныя яе падпаслядоўнасці: ![]()
2.84.
Пабудуйце прыклад паслядоўнасці, якая мае
сваімі частковымі лімітамі дадзеныя лікі: ![]() .
.
2.85.
Знайдзіце ўсе лімітавыя пункты паслядоўнасці ![]() .
.
2.86. Дакажыце, што манатонная паслядоўнасць збягаецца, калі і толькі калі збягаецца хоця б адна яе падпаслядоўнасць.
2.87.
Знайдзіце ![]() (найбольшы
частковы ліміт) і
(найбольшы
частковы ліміт) і ![]() (найменшы
частковы ліміт), калі
(найменшы
частковы ліміт), калі 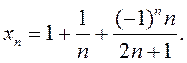
2.88.
Карыстаючыся азначэннем, дакажыце
фундаментальнасць пасля-доўнасці ![]() :
1)
:
1) ![]() ; 2)
; 2) ![]()
2.89.
Дакажыце збежнасць паслядоўнасці (![]() ) з дапамогай
крытэра Кашы, калі:
1)
) з дапамогай
крытэра Кашы, калі:
1) 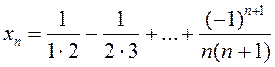 ; 2)
; 2) ![]() ; 3)
; 3) ![]()
2.90.
Сфармулюйце ў дадатным сэнсе сцверджанне, што
дадзеная пасля-доўнасць не адпавядае ўмовам крытэра Кашы. Карыстаючыся гэтай
фармулёўкай, дакажыце разбежнасць наступных паслядоўнасцяў: 1) ![]() ; 2)
; 2) 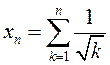 ; 3)
; 3) 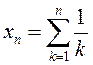 .
.
2.91.
Няхай ![]() – дадзены лік.
Знайдзіце:
1)
– дадзены лік.
Знайдзіце:
1) 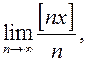 дзе
дзе ![]() цэлая частка
ліку
цэлая частка
ліку ![]() ; 2)
; 2) 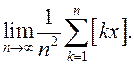
2.92.
Знайдзіце ліміты наступных паслядоўнасцяў:
1) 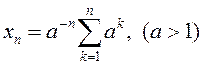 ; 2)
; 2) 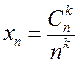 ; 3)
; 3) 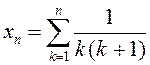 ; 4)
; 4) 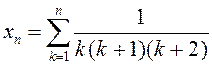 ; 5)
; 5) 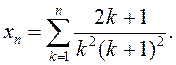
2.93.
Дакажыце:
1) ![]() калі
калі
![]() ; 2)
; 2) 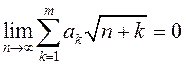 , калі
, калі 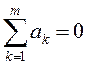 .
.
2.94.
Няхай ![]() . Знайдзіце:
1)
. Знайдзіце:
1) 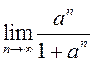 ; 2)
; 2) 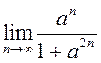 ; 3)
; 3) 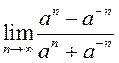 .
.
2.95.
Няхай 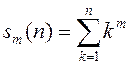 (
(![]() натуральны
лік). Знайдзіце
натуральны
лік). Знайдзіце ![]() калі:
1)
калі:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ;
4)
;
4) 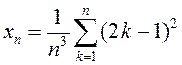 ; 5)
; 5) 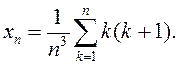
2.96.
З дапамогай крытэра Кашы дакажыце, што калі
паслядоўнасць 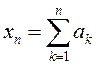 збягаецца,
то
збягаецца,
то ![]() Ці праўдзівае
адваротнае сцверджанне?
Ці праўдзівае
адваротнае сцверджанне?
2.97.
Няхай усе элементы паслядоўнасці (![]() ) з’яўляюцца
цэлымі лікамі. Дакажыце, што паслядоўнасць (
) з’яўляюцца
цэлымі лікамі. Дакажыце, што паслядоўнасць (![]() ) збягаецца, калі
і толькі калі яна фінальна сталая. (гл. задачу 2.47).
) збягаецца, калі
і толькі калі яна фінальна сталая. (гл. задачу 2.47).
2.98.
Дакажыце, што з умовы ![]() вынікае
вынікае ![]() Прывядзіце
прыклад, калі адваротнае сцверджанне не выконваецца.
Прывядзіце
прыклад, калі адваротнае сцверджанне не выконваецца.
2.99.
Дакажыце, што калі для адвольнай збежнай да
ліміту ![]() паслядоўнасці
(
паслядоўнасці
(![]() ) існуе ліміт
паслядоўнасці значэнняў функцыі (
) існуе ліміт
паслядоўнасці значэнняў функцыі (![]() (
(![]() )), то
)), то ![]() не залежыць ад
выбару (
не залежыць ад
выбару (![]() ).
).
2.100.
Дакажыце збежнасць і знайдзіце ліміт
паслядоўнасці (![]() ),
зада-дзенай рэкурэнтнай формулай
),
зада-дзенай рэкурэнтнай формулай 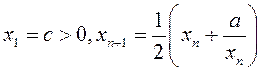 (
(![]() ).
).
2.101.
Няхай паслядоўнасць (![]() ) вызначаецца
рэкурэнтным судачы-неннем
) вызначаецца
рэкурэнтным судачы-неннем 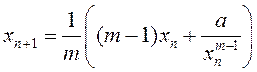 ,
дзе натуральны лік
,
дзе натуральны лік ![]() ,
, ![]() любы дадатны
лік,
любы дадатны
лік, ![]() . Дакажыце, што
. Дакажыце, што
![]()
2.102. Ці праўдзівыя наступныя сцверджанні:
1) калі ![]() то
то ![]() ; 2) калі
; 2) калі
![]() то
то ![]() ?
?
2.103.
Дакажыце наступную дастатковую ўмову збежнасці паслядоўнасці (прыкмета Д’Алямбэра): няхай элементы
паслядоўнасці ![]() і
і 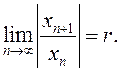 Тады: 1) калі
Тады: 1) калі
![]() то
то ![]() ; 2) калі
; 2) калі
![]() то
то ![]() Што можна
сцвярджаць у выпадку
Што можна
сцвярджаць у выпадку ![]() ?
?
2.104.
З дапамогай прыкметы Д’Алямбэра (задача 2.103)
дакажыце, што:
1) 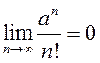 ; 2)
; 2) 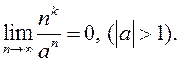
2.105.
Дакажыце наступнае сцверджанне: калі ![]() і
і 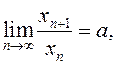 то
то ![]() Карыстаючыся
папярэднім сцверджаннем, знайдзіце:
1)
Карыстаючыся
папярэднім сцверджаннем, знайдзіце:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) 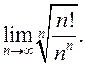
2.106.
Разгледзім паслядоўнасць (![]() ) даўжыняў
ламаных, азначаную ў задачы 2.27. Пры адвольным
) даўжыняў
ламаных, азначаную ў задачы 2.27. Пры адвольным ![]() , як вынікае з
задачы 2.27 ,
, як вынікае з
задачы 2.27 , ![]() Але
пры
Але
пры ![]() ламаныя,
відавочна, імкнуцца да гіпатэнузы трох-вугольніка. Такім чынам,
ламаныя,
відавочна, імкнуцца да гіпатэнузы трох-вугольніка. Такім чынам, ![]() дзе
дзе ![]() даўжыня гіпатэ-нузы.
Мы атрымалі, што даўжыня гіпатэнузы роўна суме даўжыняў катэтаў
трохвугольніка?!? Знайдзіце памылку ў разважанні.
даўжыня гіпатэ-нузы.
Мы атрымалі, што даўжыня гіпатэнузы роўна суме даўжыняў катэтаў
трохвугольніка?!? Знайдзіце памылку ў разважанні.
2.107.
Разгледзім паслядоўнасць ![]() даўжыняў крывых, азначаную ў задачы 2.26. Пры
даўжыняў крывых, азначаную ў задачы 2.26. Пры ![]() гэтыя крывыя
відавочна імкнуцца да адрэзка
гэтыя крывыя
відавочна імкнуцца да адрэзка ![]() .
Такім чынам,
.
Такім чынам, ![]() г.
зн.
г.
зн. ![]() ?! Знайдзіце
памылку ў разважанні.
?! Знайдзіце
памылку ў разважанні.
2.108.
Дакажыце, што ![]() грунтуючыся на
тым, што даўжыня акружыны роўна ліміту перыметраў умежаных у яе правільных
грунтуючыся на
тым, што даўжыня акружыны роўна ліміту перыметраў умежаных у яе правільных ![]() вугольнікаў пры
вугольнікаў пры
![]()
2.109.
Разгледзім паслядоўнасць камплексных лікаў ![]() Пасля-доўнасць
(
Пасля-доўнасць
(![]() ) называюць збежнай
да ліміту
) называюць збежнай
да ліміту ![]() калі
калі ![]() Дакажыце, што ўмовы
Дакажыце, што ўмовы
![]() і
і ![]() з’яўля-юцца
неабходнымі і дастатковымі ўмовамі таго, каб
з’яўля-юцца
неабходнымі і дастатковымі ўмовамі таго, каб ![]()
2.110. Даследуйце збежнасць паслядоўнасці (![]() ) і знайдзіце
ліміт, калі ён існуе: 1)
) і знайдзіце
ліміт, калі ён існуе: 1) ![]() ;
2)
;
2) ![]() ;
3)
;
3) ![]() ;
4)
;
4) 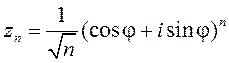 ; 5)
; 5) 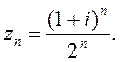
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.