► Возьмем ![]() .
Патрэбна знайсці
.
Патрэбна знайсці ![]() , каб
, каб
![]() выконвалася
няроўнасць
выконвалася
няроўнасць ![]() . Паколькі ў азначэнні
ліміта дастаткова ўказаць хоця б адзін
. Паколькі ў азначэнні
ліміта дастаткова ўказаць хоця б адзін ![]() , не абавязкова
найменшы, то дакладнае развязанне гэтай няроўнасці не патрабуецца. Відавочна,
што
, не абавязкова
найменшы, то дакладнае развязанне гэтай няроўнасці не патрабуецца. Відавочна,
што ![]() . Калі
. Калі ![]() (для гэтага
трэба ўзяць
(для гэтага
трэба ўзяць ![]() ), то і
), то і ![]() , г. зн.
, г. зн. ![]()
![]() :
: ![]() , што і
патрабавалася. Заўважым, што
, што і
патрабавалася. Заўважым, што ![]() знойдзены
з “вялікім запасам”. ◄
знойдзены
з “вялікім запасам”. ◄
►Паколькі ![]() , то
, то ![]() Атрымалі, што
пасля-доўнасць
Атрымалі, што
пасля-доўнасць ![]() адпавядае
ўмовам
адпавядае
ўмовам ![]() , дзе
, дзе ![]() а
а ![]() . Відавочна,
што
. Відавочна,
што ![]() і
і ![]() Тады, паводле
тэарэмы пра сціснутую паслядоўнасць
Тады, паводле
тэарэмы пра сціснутую паслядоўнасць ![]() ◄
◄
2.44.
Карыстаючыся
азначэннем ліміту паслядоўнасці, дакажыце, што:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) 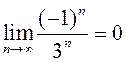 ;
4)
;
4) 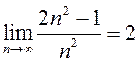 ; 5)
; 5) ![]() ; 6)
; 6) 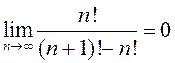 .
.
2.45.
1) Для кожнага дадзенага ![]() знайдзіце
знайдзіце ![]() , каб для
адвольнага
, каб для
адвольнага ![]() выконвалася
няроўнасць
выконвалася
няроўнасць 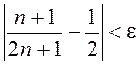 . Запоўніце
табліцу:
. Запоўніце
табліцу:
|
ε |
1 |
10– 2 |
10– 4 |
2·10– 6 |
|
N |
2) Дакажыце, што ![]() .
.
2.46. Няхай 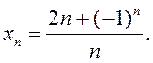 Дакажыце,
што
Дакажыце,
што ![]() вызначаючы для
кожнага
вызначаючы для
кожнага ![]() такі
такі ![]() што
што ![]() калі
калі ![]() Запоўніце
табліцу:
Запоўніце
табліцу:
|
|
0,1 |
0,01 |
0,001 |
… |
|
N |
2.47.
Паслядоўнасць ![]() называюць фінальна
сталай, калі існуе канстанта
называюць фінальна
сталай, калі існуе канстанта ![]() і
нумар
і
нумар ![]() такія, што
такія, што ![]() для ўсіх
для ўсіх ![]() . Дакажыце,што
фінальна сталая паслядоўнасць з’яўляецца збежнай. Чаму роўны яе ліміт ?
. Дакажыце,што
фінальна сталая паслядоўнасць з’яўляецца збежнай. Чаму роўны яе ліміт ?
2.48.
Няхай ![]() . Дакажыце, што
. Дакажыце, што
![]() дзе
дзе ![]() – фіксаваны натуральны
лік, іншымі словамі, адкіданне або далучэнне канечнай колькасці элементаў
збежнай паслядоўнасці не змяняе яе ліміту.
– фіксаваны натуральны
лік, іншымі словамі, адкіданне або далучэнне канечнай колькасці элементаў
збежнай паслядоўнасці не змяняе яе ліміту.
2.49.
Дакажыце, што калі ![]() , то
, то ![]() Ці заўсёды
выконваецца адваротнае сцверджанне?
Ці заўсёды
выконваецца адваротнае сцверджанне?
2.50.
Ці эквівалентнае
азначэнне ліміту паслядоўнасці (![]() )
такім азначэнням: 1)
)
такім азначэнням: 1) ![]()
![]() :
: ![]() ;
2)
;
2) ![]()
![]()
![]() ;
3)
;
3) ![]()
![]() :
: ![]() ?
?
2.51.
Няхай паслядоўнасць ![]() і лік
і лік ![]() адпавядаюць
умове:
адпавядаюць
умове: ![]() такі, што
такі, што ![]() і
і ![]() . Ці ўсякая
збежная да
. Ці ўсякая
збежная да ![]() паслядоў-насць
задавальняе гэту ўмову?
паслядоў-насць
задавальняе гэту ўмову?
2.52. Дакажыце, што ліміт збежнай паслядоўнасці не залежыць ад парадку яе элементаў, г. зн. калі ў збежнай паслядоўнасці адвольна змяніць парадак элементаў, то атрыманая паслядоўнасць будзе таксама збежнай і мець той самы ліміт, што і зыходная паслядоўнасць.
2.53.
Прывядзіце азначэнне ў
дадатным сэнсе (не выкарыстоўваючы ад-моў’е) сцверджання таго, што лік ![]() не з’яўляецца лімітам
паслядоў-насці. Дакажыце, што
не з’яўляецца лімітам
паслядоў-насці. Дакажыце, што ![]() ,
калі:
1)
,
калі:
1) ![]() ;
2)
;
2) ![]() .
.
2.54.
Сфармулюйце ў дадатным
сэнсе азначэнне таго, што паслядоўнасць разбягаецца. Дакажыце разбежнасць
паслядоўнасцяў (![]() )
)![]() 1)
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) 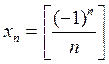 .
.
2.55.
Дакажыце, што
наступныя паслядоўнасці з’яўляюцца бясконца малымі![]() 1)
1) ![]() ;
2)
;
2) ![]() (
(![]() ); 3)
); 3) ![]() , дзе
, дзе ![]() –
– ![]() я лічба ліку
я лічба ліку ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() .
.
2.56.
Няхай ![]() – бясконца
малая паслядоўнасць і
– бясконца
малая паслядоўнасць і ![]()
![]() . Дакажыце, што
паслядоўнасць
. Дакажыце, што
паслядоўнасць ![]() дзе
дзе ![]() будзе таксама
бясконца малой.
будзе таксама
бясконца малой.
2.57.
Дакажыце, што:
1) ![]()
![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]()
![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() калі
калі ![]() ; 6)
; 6) ![]() калі
калі ![]() .
.
2.58. Ці праўдзівыя сцверджанні: 1) усякая бясконца вялікая паслядоў-насць з’яўляецца неабмежаванай; 2) усякая неабмежаваная пасля-доўнасць з’яўляецца бясконца вялікай?
2.59.
Карыстаючыся тэарэмай 1, знайдзіце ліміт
паслядоўнасці: 1) 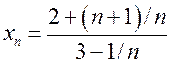 ;
2)
;
2) 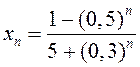 ;
3)
;
3) 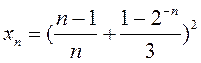 ; 4)
; 4) 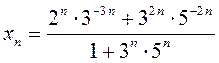 .
.
2.60.
Раскрыйце нявызначанасць ![]() (г. зн. знайдзіце
ліміт паслядоўна-сці
(г. зн. знайдзіце
ліміт паслядоўна-сці ![]() )
шляхам папярэдняга дзялення лічніка і назоўніка дробу на адпаведную ступень
)
шляхам папярэдняга дзялення лічніка і назоўніка дробу на адпаведную ступень ![]() або
або ![]() :
:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.