2.168.
Падайце прыклады
бясконца вялікіх пры ![]() функцый,
якія задавальняюць умовы папярэдняй задачы.
функцый,
якія задавальняюць умовы папярэдняй задачы.
2.169.
Вызначце парадак
бясконца малых функцый пры ![]() :
1)
:
1) ![]() ; 2)
; 2)
![]() ;
3)
;
3) ![]() ;
4)
;
4) ![]() ;
5)
;
5) ![]() ; 6)
; 6) ![]() ;
7)
;
7) ![]() .
.
2.170.
Вызначце парадак бясконца
вялікіх функцый ![]() :
1)
:
1) 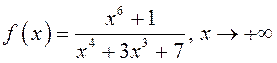 ; 2)
; 2) ![]() ;
3)
;
3) 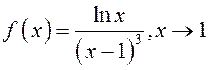 ; 4)
; 4)
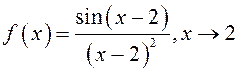 ;
5)
;
5) ![]() ; 6)
; 6)
![]() .
.
2.171.
Падайце прыклады
функцый ![]() , для якіх
выконваюцца сцверджанні:
1)
, для якіх
выконваюцца сцверджанні:
1) ![]() ; 2)
; 2) ![]() ;
3)
;
3) ![]() ; 4)
; 4) ![]() .
.
2.172.
Няхай функцыя ![]() і
і ![]() пры
пры ![]() . Вызначце,
якія з наступных функцый будуць бясконца малымі пры
. Вызначце,
якія з наступных функцый будуць бясконца малымі пры ![]() больш высокага
парадку, чым
больш высокага
парадку, чым ![]() :
1)
:
1) ![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() ; 4)
; 4)
![]() ; 5)
; 5)
![]() ;
6)
;
6) ![]() ; 7)
; 7) ![]() ; 8)
; 8) ![]() ; 9)
; 9) ![]() .
.
2.173.
Ці выконваецца
роўнасць ![]() пры
пры ![]() , калі:
1)
, калі:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
2.174.
Няхай ![]() пры
пры ![]() . Дакажыце,
што:
1)
. Дакажыце,
што:
1)![]() ; 2)
; 2)![]() ; 3)
; 3)![]() ; 4)
; 4)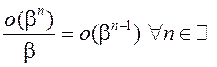 ; 5)
; 5)![]() ; 6)
; 6)![]() ;
7)
;
7)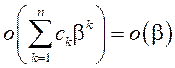 (
(![]() – любыя лікі).
– любыя лікі).
2.175.
Няхай ![]() і
і ![]() – натуральныя
лікі, прычым
– натуральныя
лікі, прычым ![]() . Дакажыце, што
пры
. Дакажыце, што
пры ![]() :
1)
:
1) ![]() ; 2)
; 2) ![]() ;
3)
;
3) ![]() ; 4)
; 4) ![]() .
.
2.176.
Дакажыце, што:
1) ![]() ; 2)
; 2) ![]() ;
3)
;
3) ![]() ; 4)
; 4) ![]() ;
5)
;
5) ![]() ; 6)
; 6) ![]() .
.
2.177.
Няхай ![]() і
і ![]() . Дакажыце,
што:
1)
. Дакажыце,
што:
1) ![]() 2)
2) ![]() .
.
2.178.
Дакажыце, што пры
дастаткова вялікім ![]() маюць
месца няроўна-сці:
1)
маюць
месца няроўна-сці:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
2.179.
Якія з наступных
бясконца малых функцый эквівалентныя бясконца малой ![]() :
1)
:
1) ![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() ; 7)
; 7) ![]() ?
?
2.180.
Няхай ![]() пры
пры ![]() . Выберыце з
пададзеных ніжэй функцый пары бясконца малых, эквівалентных паміж сабой:
1)
. Выберыце з
пададзеных ніжэй функцый пары бясконца малых, эквівалентных паміж сабой:
1) ![]() ; 2)
; 2)
![]() ; 3)
; 3)
![]() ; 4)
; 4) ![]() ;
5)
;
5) ![]() ; 6)
; 6) ![]() ; 7)
; 7) ![]() ; 8)
; 8) ![]() .
.
2.181.
Дакажыце крытэр
эквівалентнасці: ![]() пры
пры ![]() калі і толькі
калі
калі і толькі
калі ![]() .
.
2.182.
Дакажыце сцверджанні:
1) калі ![]() пры
пры ![]() і
і ![]() , то
, то ![]() пры
пры ![]() ; 2) калі
; 2) калі
![]() пры
пры ![]() і
і ![]() , то
, то ![]() пры
пры ![]() .
.
2.183.
Няхай ![]() . Дакажыце,
што:
1)
. Дакажыце,
што:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
2.184.
Знайдзіце, пры якіх
значэннях ![]() і
і ![]() функцыі
функцыі ![]() і
і ![]() будуць
эквівалентнымі:
1)
будуць
эквівалентнымі:
1) ![]() ;
2)
;
2) ![]() ;
3)
;
3)![]() ; 4)
; 4)![]() .
.
2.185. Дакажыце сцверджанне: калі ![]() ,
, ![]() пры
пры ![]() і існуе
і існуе 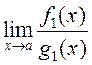 , то існуе
, то існуе 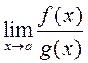 , прычым гэтыя
ліміты роўныя паміж сабой (іншымі словамі, пры знаходжанні ліміту дзелі лічнік
і назоўнік можна замяніць эквівалентнымі функцы-ямі).
, прычым гэтыя
ліміты роўныя паміж сабой (іншымі словамі, пры знаходжанні ліміту дзелі лічнік
і назоўнік можна замяніць эквівалентнымі функцы-ямі).
2.186. Няхай ![]() пры
пры ![]() . Ці можна ў ліміце
. Ці можна ў ліміце 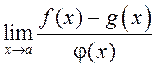 замяніць
замяніць ![]() на
на ![]() , г. зн. сцвярджаць,
што
, г. зн. сцвярджаць,
што
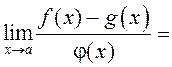
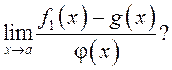 Улічваючы, што
пры
Улічваючы, што
пры ![]() функцыі
функцыі ![]() і
і ![]() ёсць
эквівалентныя, раз-гледзьце прыклады:
а)
ёсць
эквівалентныя, раз-гледзьце прыклады:
а) ![]() , б)
, б)
![]() .
.
2.187.
Знайдзіце памылку ў
наступным сцверджанні: калі ![]() пры
пры
![]() і існуе
і існуе 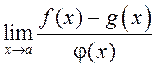 , то гэты ліміт
заўсёды роўны нулю, паколькі
, то гэты ліміт
заўсёды роўны нулю, паколькі 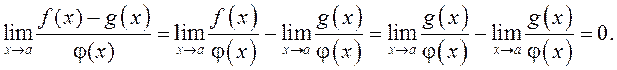 (параўнайце
з задачай 2.186. б)).
(параўнайце
з задачай 2.186. б)).
2.188.
Дакажыце наступныя
асімптатычныя формулы пры ![]() :
1)
:
1) ![]() ;
2)
;
2) 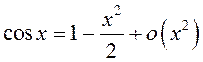 ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() ; 7)
; 7) ![]() .
.
2.189.
Атрымайце
асімптатычныя формулы пры ![]() з
рэшткавым складнікам тыпу
з
рэшткавым складнікам тыпу ![]() для
наступных функцый: 1)
для
наступных функцый: 1) ![]() ;
2)
;
2) ![]() ; 3)
; 3)
![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() ; 7)
; 7) ![]() ; 8)
; 8)
![]() .
.
2.190.
Запішыце асімптатычныя
формулы пры ![]() з рэшткавым
складнікам тыпу
з рэшткавым
складнікам тыпу ![]() для
наступных функцый:
1)
для
наступных функцый:
1)![]() ; 2)
; 2)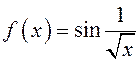 ;
3)
;
3)![]() ; 4)
; 4)![]() .
.
2.191.
Знайдзіце ліміты:
1)![]() ; 2)
; 2)
![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() ; 7)
; 7) 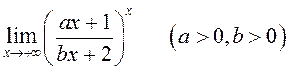 ; 8)
; 8) 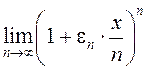 , дзе
, дзе ![]() ; 9)
; 9) ![]() .
.
2.192.
Знайдзіце ліміты:
1) ![]() ; 2)
; 2)
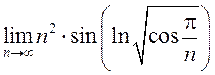 ;
3)
;
3) 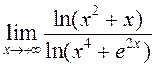 ; 4)
; 4) 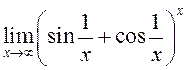 .
.
2.193. Лік ![]() называюць
частковым лімітам функцыі
называюць
частковым лімітам функцыі ![]() пры
пры ![]() , калі існуе
паслядоўнасць
, калі існуе
паслядоўнасць ![]() ,
такая, што
,
такая, што ![]() і
і ![]() . Аналагічна
вызначаюць бясконцыя частковыя лімі-ты. Знайдзіце ўсе частковыя ліміты функцыі
. Аналагічна
вызначаюць бясконцыя частковыя лімі-ты. Знайдзіце ўсе частковыя ліміты функцыі ![]() пры
пры ![]() .
.
2.194.
Найбольшы (найменшы)
частковы ліміт функцыі ![]() пры
пры ![]() называюць верхнім
( ніжнім ) лімітам
называюць верхнім
( ніжнім ) лімітам ![]() і абазначаюць
і абазначаюць ![]() . Знайдзіце:
1)
. Знайдзіце:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]()
![]() .
.
2.195.
Дакажыце, што для
існавання ліміта ![]() неабходна
і дастаткова, каб
неабходна
і дастаткова, каб ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.